Методика аналогового моделирования динамических объектов, страница 5

На этом этапе встаёт вопрос порядоковое расхождение постоянных времени линейной части системы. Так как реализация системы подразумевается с использованием одинаковых или близких по показателям ОУ, то питание общей схемы не будет проблемой, но проблематично реализовывать систему, в которой постоянные времени расходятся на несколько порядков. На пример, реализация системы с расхождением двух постоянных на три-четыре порядка потребует разницы между номиналами реализующих их элементов на те же три-четыре порядка. Различное тепловыделение, различие допусков (для одного конденсатора допуск может быть незначительным, а для другого такая же величина будет составлять практически весь его номинал) приводит к увеличению погрешностей, ошибкам, повреждениям при эксплуатации. К тому же защита меньшего по размерам и номиналу элемента электрической схемы может быть незначительной по сравнению с воздействием на него (температурным, магнитным и электрическим полем) значительно болшего номиналом и размерами элемента.

Учитывая все перечисленные факторы, примем четыре группы постоянных времени:

¨  10^-6 - 10^-4;

¨  10^-3 - 10^-1;

¨  10⁰ – 10²;

¨  10³ – 10⁵.

Далее необходимо из звеньев, постоянные времени которых пренадлежат к какой либо из групп сформировать набор звеньев, порядок которых не будет превышать 2.

Также нужно учесть, что не существует резистора или конденсатора с любым номиналом. Все выпускаемые электрические элементы имеют нормированные номиналы, сведённые в ряды. Каждый ряд имеет своё название и набор номиналов. Из этих номиналов и следует набирать резистивные и ёмкостные элементы конечной схемы, суммируя их для получения требуемой величины.

После того как было проведено разбиение на группы, а далее на звенья, можно приступать к составлению конечной схемы. Схема составляется по следующим правилам:

­  колличество вычислительных блоков должно быть как можно меньшим;

­  все элементы должны быть одного или близкого по допускам и приминению типа;

­  желательно использовать высокоточные электрические элементы;

­  соединительные проводники сокращаются до минимума;

­  нежелательно использовать б/у и просроченные элементы, а также элементы, получившие в процессе сборки тепловые и физические повреждения;

­  необходимо располагать звенья конечной схемы в порядке возрастания порядка постоянных времени, составляющих звено.

Эти правила являются основными для аналогового моделирования и помогают получить наиболее точную реализацию системы с наименьшей погрешностью. Однако, в аналоговых вычислительных машинах и комплексах они учитываются при заводсткой сборке и наладке, и учитывать при наборе схемы на  АВМ необходимо только первое и последнее правила.

Таким образом обобщённый метод составления аналоговых схем можно представить в виде следующей структуры:

 

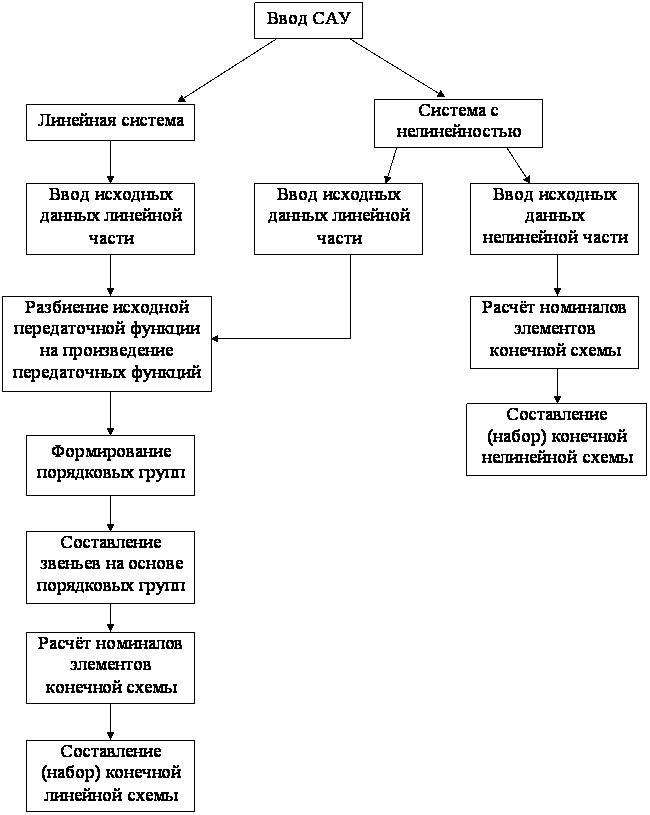
Рис. 3.8. Структура обобщенного метода аналогового моделирования

3.3 Пример аналогового моделирования.

Для примера рассмотрим реализацию нескольких разных систем.

Пример 1: Исходные данные:

Система линейная незамкнутая, передаточная функция: .

Задача: составить аналоговую модель системы.

Для решения задачи обратимся к приведённой выше структуре и увидим, что передаточная функция соответствует условиям реализации – порядок не превышает 2.

Разобъём знаменатель на скобки:

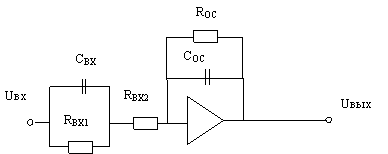Полученная передаточная функция соответсвует последовательному соединению форсирующего и аппериодического 2-го порядка (или двух инерционных) звеньев. В пункте 2.1.11 главы 2 можно найти схему этого звена и формулы её расчёта: