Результаты расчетов сводим в таблицу. Вал вычерчиваем в определенном масштабе. Масштаб длины выберем 1:5. Выбираем масштаб сил 1 см=300 кг и строим многоугольник сил. Полюсное расстояние выбираем произвольно равным 15 см. В масштабе сил оно равно 4500 кг. Под схемой вала строим веревочный многоугольник. Изоюражающий эпюру изгибающих моментов.
|
№ участка вала |
Диаметр вала, |
Длина участка
вала, |
Объем, V, м3 |
Сила, действующая на вал, G, кг |
|
1 |
||||
|
2 |
||||
|
3 |
||||
|
4 |
||||
|
5 |
||||
|
6 |
||||
|
7 |
||||
|
8 |
||||
|
9 |
||||
|
10 |
||||
|
11 |
||||
|
12 |
||||
|
13 |
||||
|
14 |
||||
|
15 |
||||
|
16 |
||||
|
17 |
||||
|
18 |
Величину
изгибающего момента в любой точке вала можно найти, умножив соответствующую
ординату эпюры Z, измеренную в масштабе длин на полюсное расстояние Н1.
Теперь предполагаем, что вал нагружен фиктивной сплошной нагрузкой, которую
изображаетэпюра изгибающих моментов. Так как вал имеет переменный диаметр, то
полюсное расстояние Нz в
многоугольнике фиктивных сил, которое должно быть равно жесткости вала ![]() ,
,
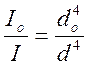 , где
, где 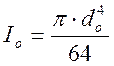 ,
отношение модулей упругости
,
отношение модулей упругости Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.