Расчет центробежного насоса (число оборотов насоса = 3000 об/мин), страница 2

,                                              (2.1)

где     - плотность перекачиваемой среды;

- ускорение свободного падения;

, м – напор насоса (из табл.1.1);

, л/с – подача насоса (из табл.1.1).

Характеристика сети:

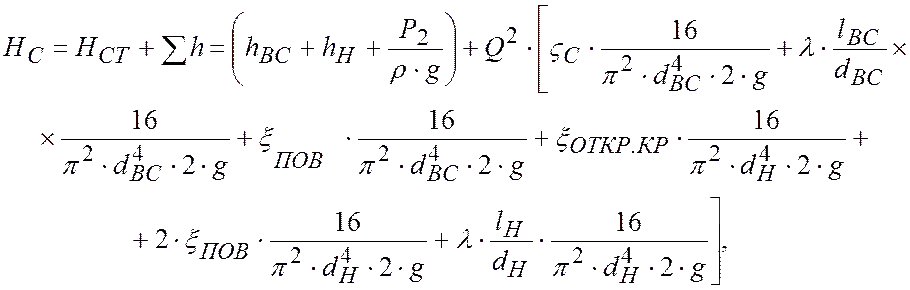(2.2)

где   ζc – коэффициент гидравлического сопротивления сетки бака 1, ζc = 3;

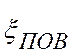         -  коэффициент гидравлического сопротивления поворота на всасе, 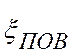= 1,265;

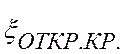        - коэффициент гидравлического сопротивления полностью открытого крана, .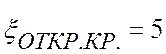

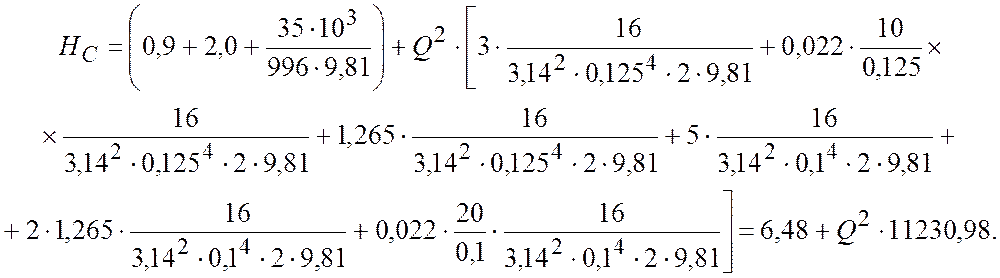
(2.3)

Строим характеристику сети (рис.2).

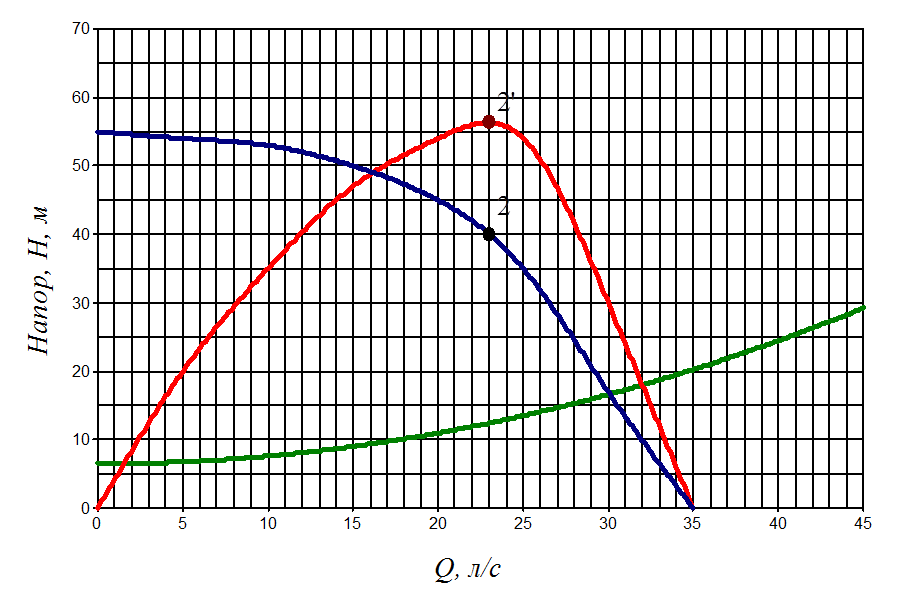
Рис.2. Характеристика сети.

Основные параметры рабочей точки насоса:

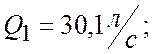
Полезная мощность насоса:

 ;                                               (2.4)

Затраченную мощность:

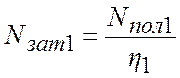;                                                    (2.5)

.

2.2.  Как изменить диаметр трубопровода, чтобы КПД насоса был максимальным?

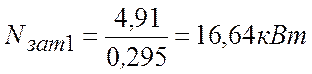Из рис.2 определяем характеристики насоса при максимальном КПД (точка 2):

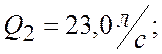
Подставляем данные значения характеристик насоса при максимальном КПД в уравнение (2.2) и решаем относительно .

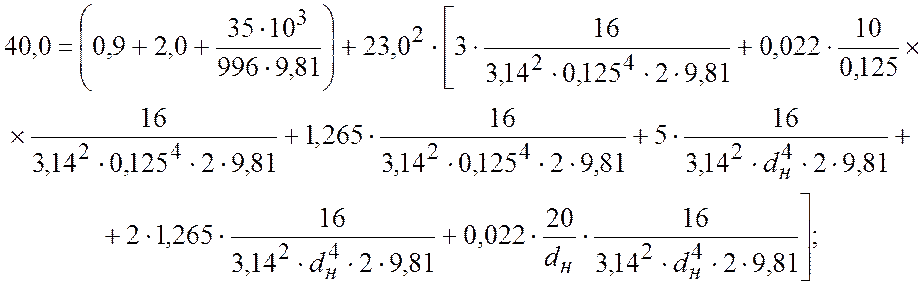
(2.6)

Диаметр нагнетательного трубопровода:  

Таким образом найденный диаметр удовлетворяет требуемому условию .

2.3.  Как нужно изменить обороты двигателя, чтобы производительность насоса увеличилась на α = 5%? Определить в этом режиме .

Новая производительность насоса:

                                                     (2.7)

.

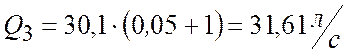Соответственно напор на характеристике трубопровода составит

Уравнение параболы подобных режимов:

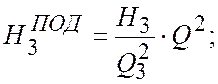                                                 (2.8)

.

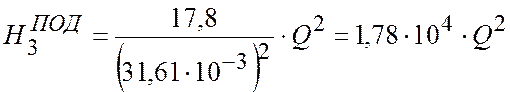Строим параболу подобных режимов (рис.3).

По рис.3 определяем производительность в точке пересечения параболы подобия с характеристикой насоса (точка 3').

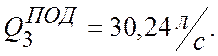
Точка 3 – точка пересечения параболы подобных режимов с характеристикой трубопровода. Точки 3’ и 3 подобны, так как расположены на одной кривой подобия, значит для них справедливо выражение:

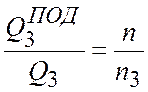                                                          (2.9)

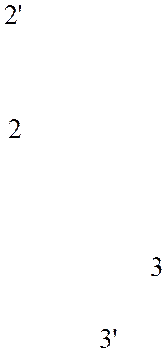
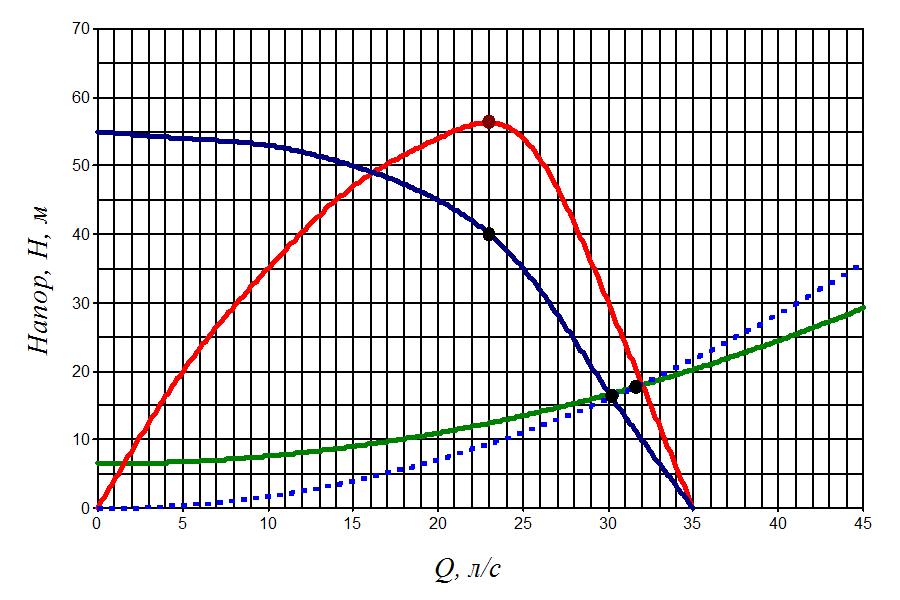
Рис.3. Характеристика сети при увеличении производительности на 5%.

КПД насоса в данном режиме определяется точкой 3' и составляет  

Полезная мощность насоса, аналогично формуле (2.4):

;

Затраченная мощность:

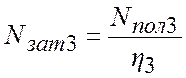;                                                  (2.10)

2.4.  После частичного закрытия крана (коэффициент гидравлического сопротивления ), определить .

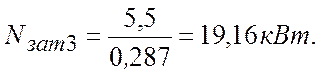
Составляем характеристику сети при частично закрытом кране, аналогично формуле (2.2).

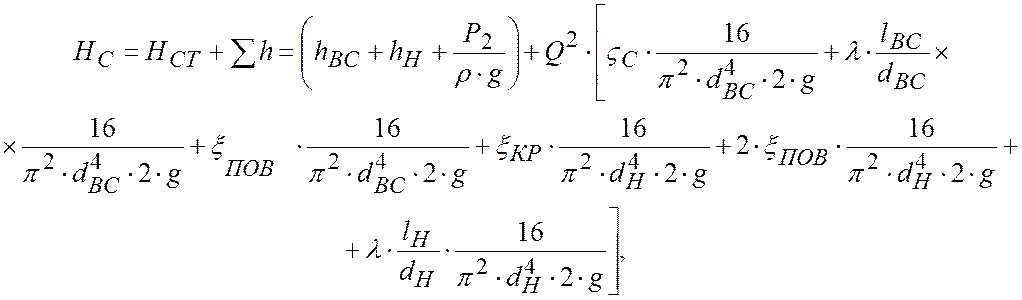
Точка 4 – новая рабочая точка, при частично закрытом кране. В этой точке определяем расход, напор и КПД (рис.4):

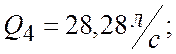
Полезная мощность насоса, аналогично формуле (2.4):

Затраченная мощность, аналогично формуле (2.10):

;

 

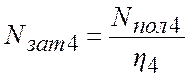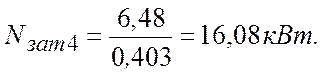
Соответствующая характеристика сети представлена на рис.4.

 

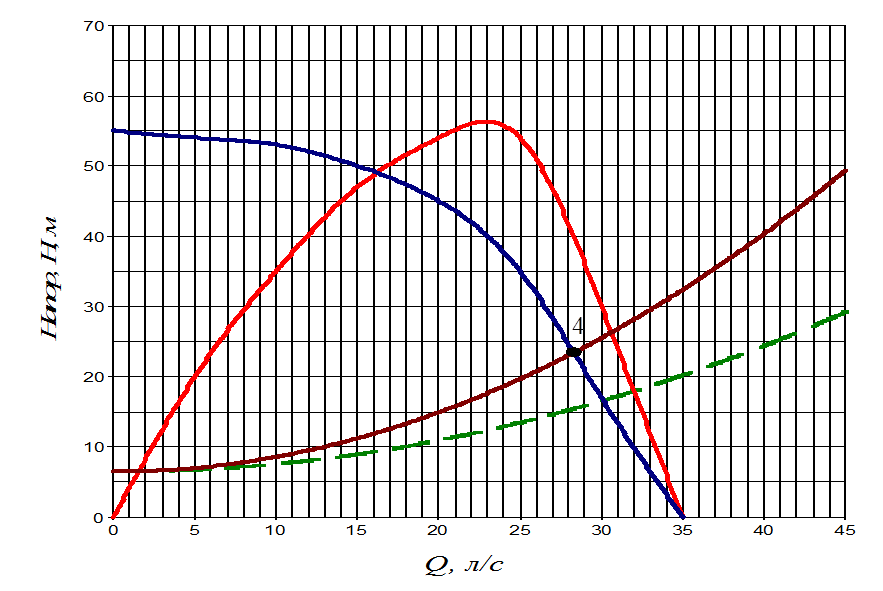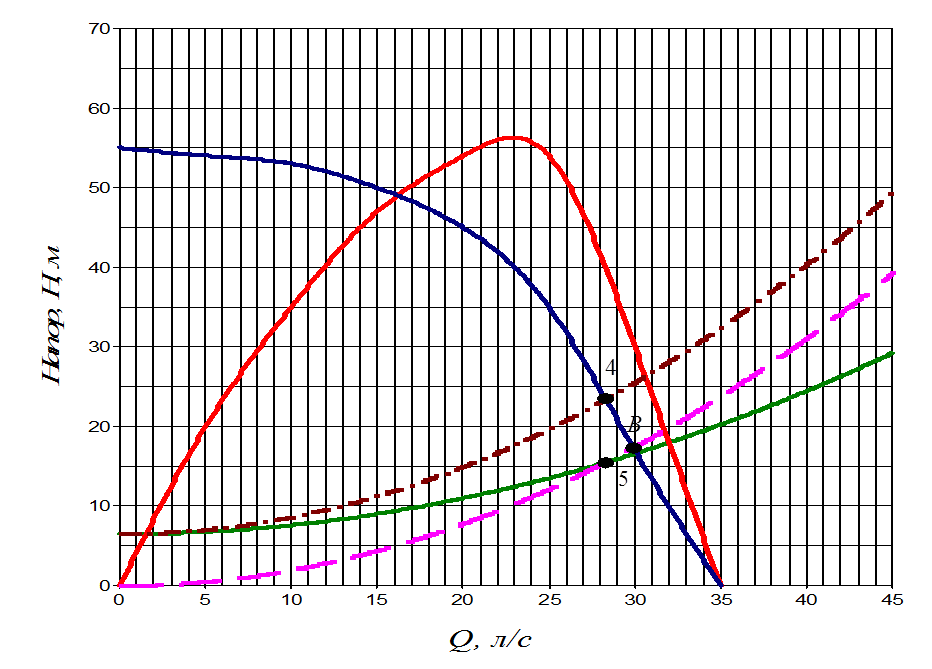
Рис.4. Характеристика сети при частично закрытом кране.

2.5.  Как надо изменить обороты двигателя, чтобы получить такой же расход, который получился при частичном закрытии крана, работая на ту же сеть при полном открытии крана и определить .

Принимаем производительность 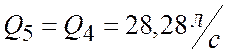. При данном расходе определяем соответствующий напор на характеристике сети при полностью открытом кране (точка 5).

Уравнение параболы подобия в этом случае, аналогично формуле (2.8):

.

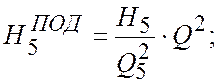
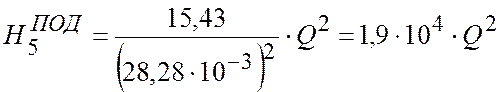Парабола подобных режимов пересекает характеристику насоса в точке В.

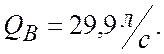
Точки 5 и В подобны, следовательно имеет место тождество, аналогичное (2.9)

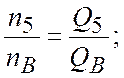
где 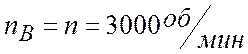 - частота вращения основного насоса;

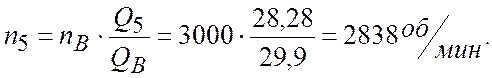
КПД насоса в данном режиме будет равно КПД, соответствующему точке 5,

Полезная мощность насоса, аналогично формуле (2.4):

;

Затраченная мощность, аналогично формуле (2.10):

;

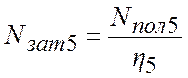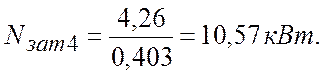
Характеристика сети на соответствующем режиме представлена на рис.5.