Изучение возможности аппроксимации сигнала многочленом Фурье по ортогональной системе гармонических функций, страница 4

2. Нахождение спектров амплитуд и начальных фаз колебания с тональной амплитудной модуляцией.

Исходные данные амплитудно-модулированных сигналов:

амплитуда несущего колебания – , частота несущего колебания – , частота модулирующего сигнала при тональной модуляции - , начальные фазы колебаний - , коэффициент модуляции –  и .

Синтез колебания с тональной амплитудной модуляцией при коэффициенте модуляции 0,5.

Модулирующий сигнал:

.

В этом случае спектр амплитудно-модулированного колебания состоит из трех гармонических составляющих – несущей, нижней боковой и верхней боковой:

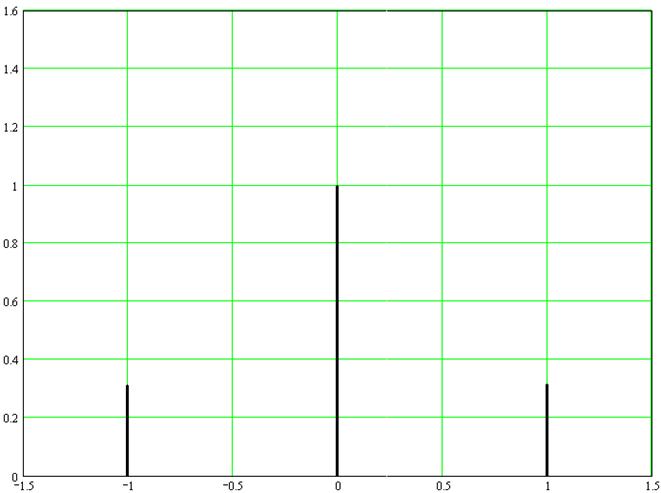
Рисунок 11 - Амплитудный спектр колебания с тональной амплитудной модуляцией при коэффициенте модуляции 0,5

Синтез колебания с тональной амплитудной модуляцией при коэффициенте модуляции 1.

Модулирующий сигнал:

.

В этом случае спектр амплитудно-модулированного колебания состоит из трех гармонических составляющих – несущей, нижней боковой и верхней боковой:

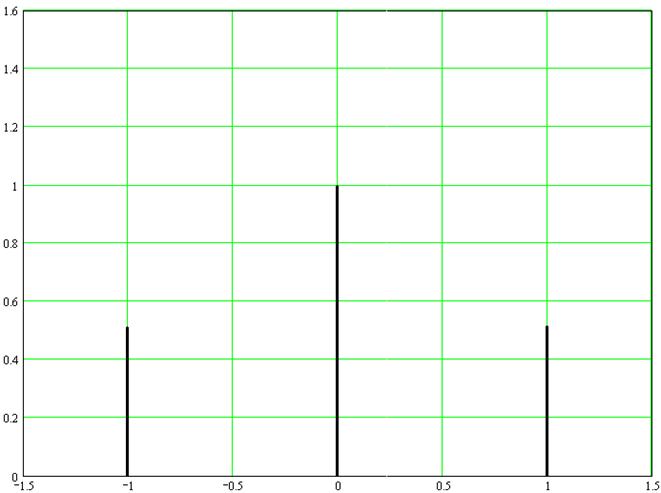
Рисунок 12 - Амплитудный спектр колебания с тональной амплитудной модуляцией при коэффициенте модуляции 1

3. Формирование сигналов с использованием пакета Electronics Workbench.

3.1 Формирование прямоугольных видеоимпульсов.

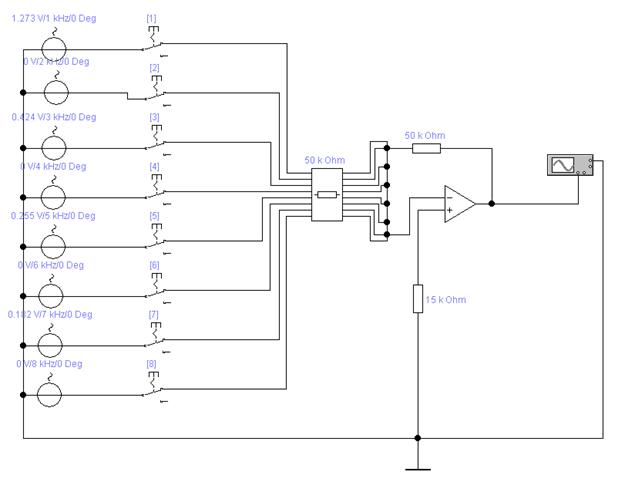
Рисунок 13 - Схема для формирования прямоугольных видеоимпульсов

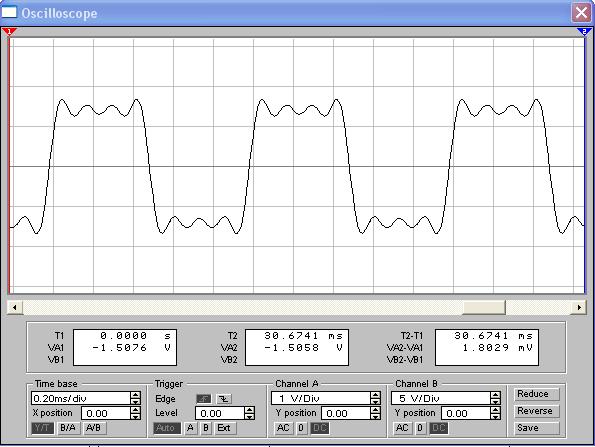
Рисунок 14 - Прямоугольные видеоимпульсы, сформированные в Electronics Workbench

3.2 Формирование треугольных видеоимпульсов.

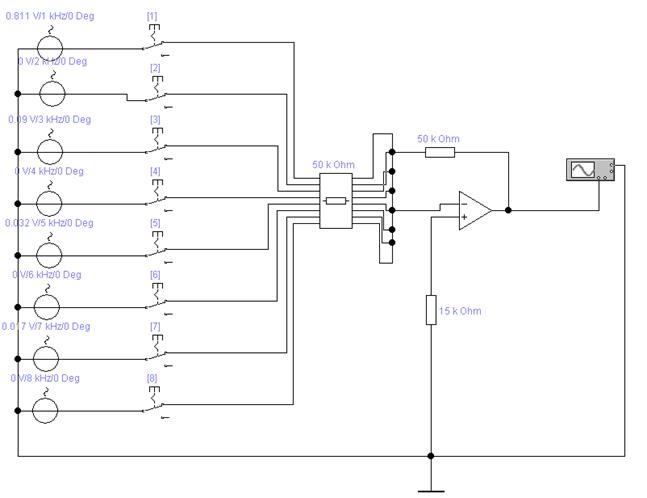
Рисунок 15 - Схема для формирования треугольных видеоимпульсов

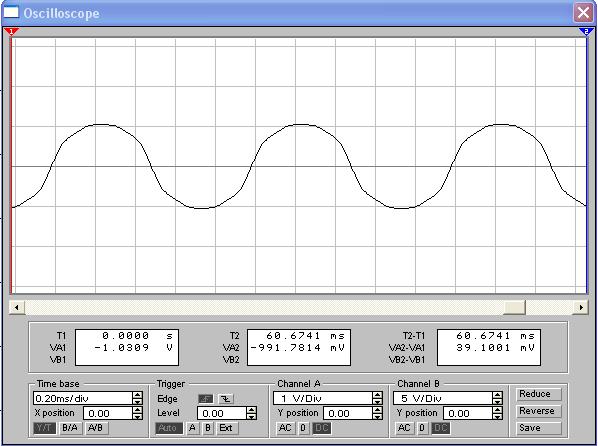
Рисунок 16 - Треугольные видеоимпульсы, сформированные в Electronics Workbench

3.3 Формирование пилообразных видеоимпульсов.

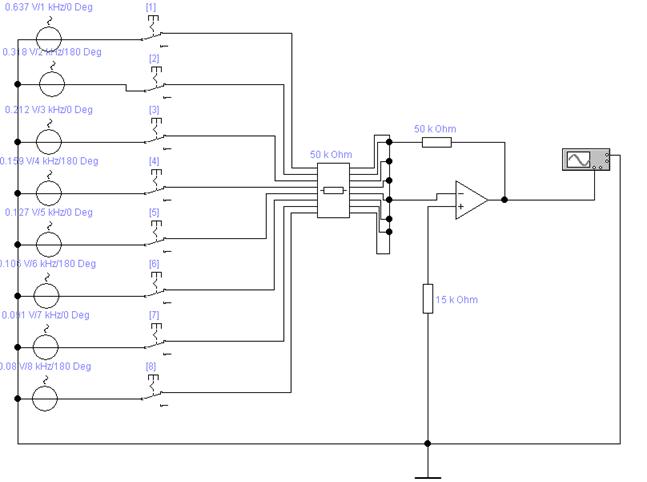
Рисунок 17 - Схема для формирования пилообразных видеоимпульсов

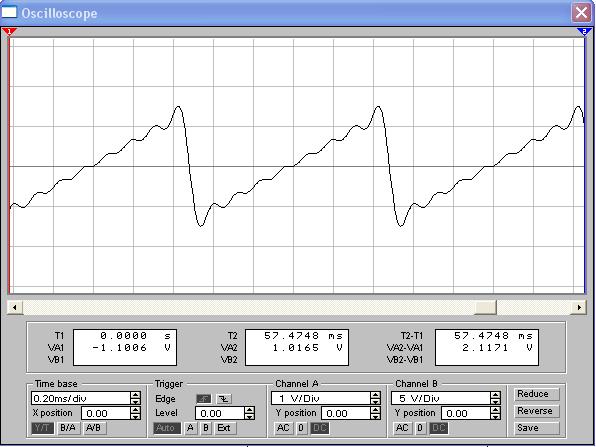
Рисунок 18 - Пилообразные видеоимпульсы, сформированные в Electronics Workbench

4. Выводы.

Изучили возможности аппроксимации сигнала многочленом Фурье по ортогональной системе гармонических функций. Провели анализ периодических сигналов, построили для 3 детерминированных сигналов, их амплитудные и фазовые спектры в MathCAD и исследовали эти амплитудные и фазовые спектры периодических последовательностей прямоугольных, треугольных и пилообразных видеоимпульсов. Смоделировав сигналы в пакете Electronics Workbench восемью гармониками, и сравнили результаты, полученные в пакете Mathcad: они практически полностью совпадают, что подтверждает возможность использования для аппроксимации сигналов многочлена Фурье по ортогональной системе гармонических функций. Незначительные расхождения графиков в пакете Mathcad и пакете Electronics Workbench можно объяснить различной точностью этих двух программ.