Изучение возможности аппроксимации сигнала многочленом Фурье по ортогональной системе гармонических функций, страница 2

Рисунок 2 - Периодическая последовательность прямоугольных видеоимпульсов

|а(k)|, B

             

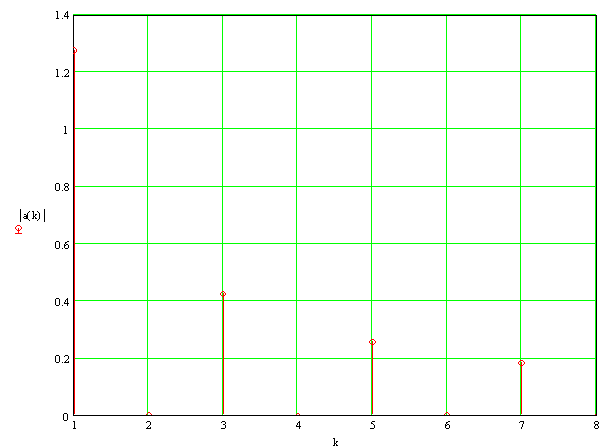
Рисунок 3 - Амплитудный спектр периодической последовательности

прямоугольных видеоимпульсов

φ(k), рад

           

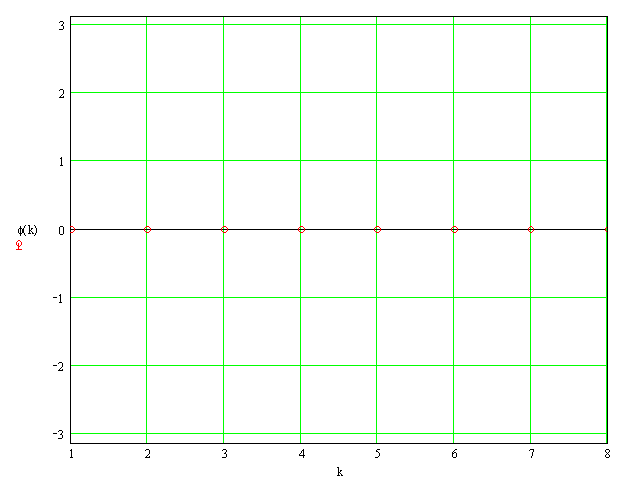
Рисунок 4 - Фазовый спектр  периодической последовательности

прямоугольных видеоимпульсов

1.2 Нахождение спектров периодической последовательности треугольных видеоимпульсов  (рис.1.б).

По заданной последовательности прямоугольных импульсов (рис. 1.б) на интервале времени, равном периоду, составим ее условие существования:

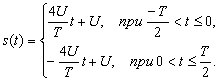
Разложим сигнал в тригонометрический ряд Фурье - для этого найдем коэффициенты ряда  и :

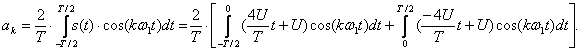  (4)

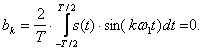
После преобразования коэффициента ряда  - замены  - получим следующее выражение:

Используя предыдущую формулу, найдем коэффициент ряда , при k=0:

                                                                     (5)

Подставим значение коэффициент ряда (5) в формулу сигнала (3) и получим:

На рис.5,6,7 представлены: периодическая последовательность треугольных видеоимпульсов, ее амплитудный и фазовый спектры.

s(t), B

t, c

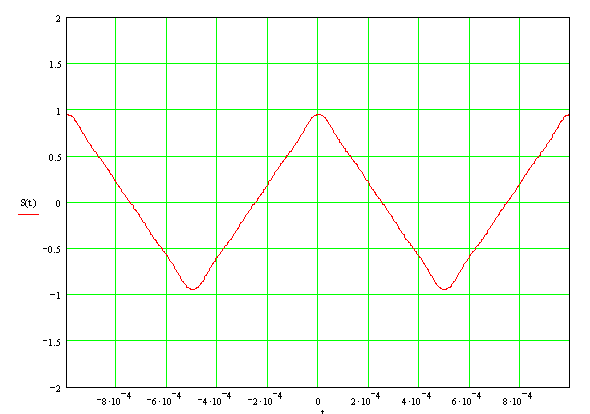
Рисунок 5 - Периодическая последовательность треугольных видеоимпульсов

|а(k)|, B

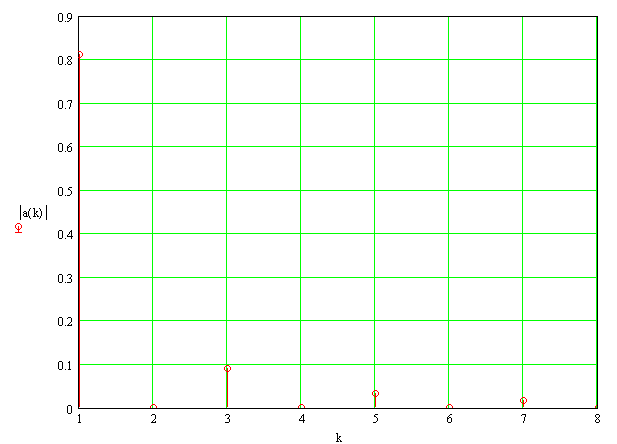
Рисунок 6 - Амплитудный спектр  периодической последовательности

треугольных видеоимпульсов

φ(k), рад

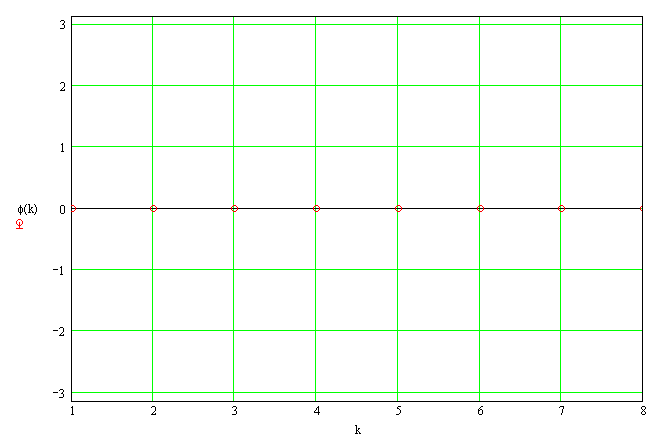
Рисунок 7 - Фазовый спектр  периодической последовательности