МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
РОССИЙСКОЙ ФЕДЕРАЦИИ
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Физический факультет
Кафедра общей физики
Кислер Дмитрий Владимирович
ОТЧЕТ
О лабораторной работе № 1.1
«Статистические закономерности, возникающие при измерениях»
Измерительный практикум, 1 курс, группа 7361
Преподаватель измерительного практикума
_________________ Климкин В.Ф.
«__»_____________ 2007 г.
Новосибирск, 2007 г.
Цель работы: Ознакомление с методами обработки результатов измерений. Проверка статистических закономерностей. Определение закона распределения для потока α-частиц, возникающих про радиоактивном распаде ядер.
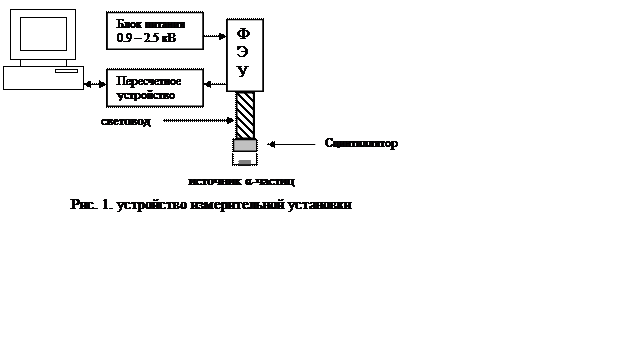 |
Краткое описание: α-частицы, вылетающие из источника вследствие радиоактивного распада, попадают в сцинтиллятор и вызывают вспышки света определенной частоты. Именно той, которую пропускает световод. Далее, по световоду свет попадает в ФЭУ (ФотоЭлектронный Умножитель), который сопряжен с компьютером. При оптимальном напряжении отношение сигнал/шум максимальное.
 Если измеряемая величина x принимает
непрерывный ряд значений, а случайные ошибки измерений обусловлены большим
числом малых и независимых друг от друга отклонений, то плотность вероятности p
измеряемых значений x относительное наиболее вероятного (среднего)
Если измеряемая величина x принимает
непрерывный ряд значений, а случайные ошибки измерений обусловлены большим
числом малых и независимых друг от друга отклонений, то плотность вероятности p
измеряемых значений x относительное наиболее вероятного (среднего) ![]() описывается нормальным распределением
(Гаусса):
описывается нормальным распределением
(Гаусса): 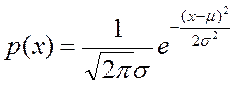 , где
, где ![]() –
стандартное отклонение,
–
стандартное отклонение, ![]() – дисперсия.
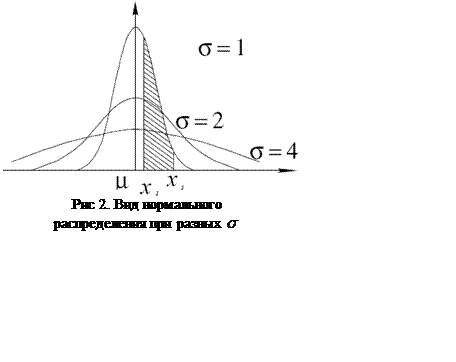
– дисперсия. ![]() служит основным параметром, определяющим
вид кривой распределения случайных величин (рис. 1). Площадь фигуры,
заключенной между кривой осью x и двумя координатами x1 и x2, численно равна
вероятности, с которой значение случайной величины попадает в интервал x2 – x1.Вся площадь под
кривой равна единице. При нормальном распределении значение случайной величины
попадает в интервал
служит основным параметром, определяющим
вид кривой распределения случайных величин (рис. 1). Площадь фигуры,
заключенной между кривой осью x и двумя координатами x1 и x2, численно равна
вероятности, с которой значение случайной величины попадает в интервал x2 – x1.Вся площадь под
кривой равна единице. При нормальном распределении значение случайной величины
попадает в интервал ![]() с вероятностью 0,68, в интервал
с вероятностью 0,68, в интервал ![]() – с вероятностью 0,95, в интервал
– с вероятностью 0,95, в интервал ![]() – с вероятностью 0,997.
– с вероятностью 0,997.
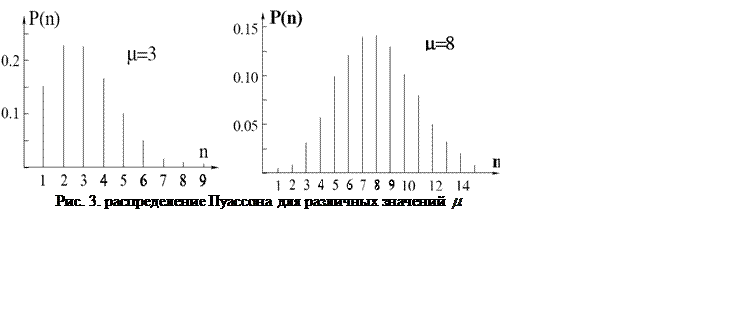 |
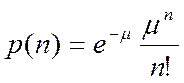 , где p(n) – вероятность появления значения n,
, где p(n) – вероятность появления значения n, С ростом ![]() распределение Пуассона
становится более симметричным и похожим на распределением Гаусса:
распределение Пуассона
становится более симметричным и похожим на распределением Гаусса: 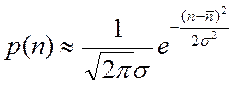 , где
, где ![]() .
Различие становится малым при
.
Различие становится малым при ![]() .
.
Критерий
![]() – это критерий согласия теоретического
распределения с экспериментальными данными. Определяется соотношением:
– это критерий согласия теоретического
распределения с экспериментальными данными. Определяется соотношением: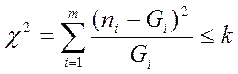 , где
, где ![]() –измеряемое
число событий в бине в котором величина,
–измеряемое
число событий в бине в котором величина, ![]() –
значение предлагаемого теоретического распределения. В этом соотношении
–
значение предлагаемого теоретического распределения. В этом соотношении![]() сравнивается с числом степеней свободы k
= (m – C), где m – число бинов гистограммы, С – число связей (для
распределения Гаусса равно 2, для распределения Пуассона 1).
сравнивается с числом степеней свободы k
= (m – C), где m – число бинов гистограммы, С – число связей (для
распределения Гаусса равно 2, для распределения Пуассона 1).
В
соответствии с критерием ![]() , согласие между
теоретическим распределением и экспериментальной выборкой можно считать
удовлетворительным, если
, согласие между
теоретическим распределением и экспериментальной выборкой можно считать
удовлетворительным, если ![]() . В противном случае соответствие
эксперимента и теории сомнительно.
. В противном случае соответствие
эксперимента и теории сомнительно.
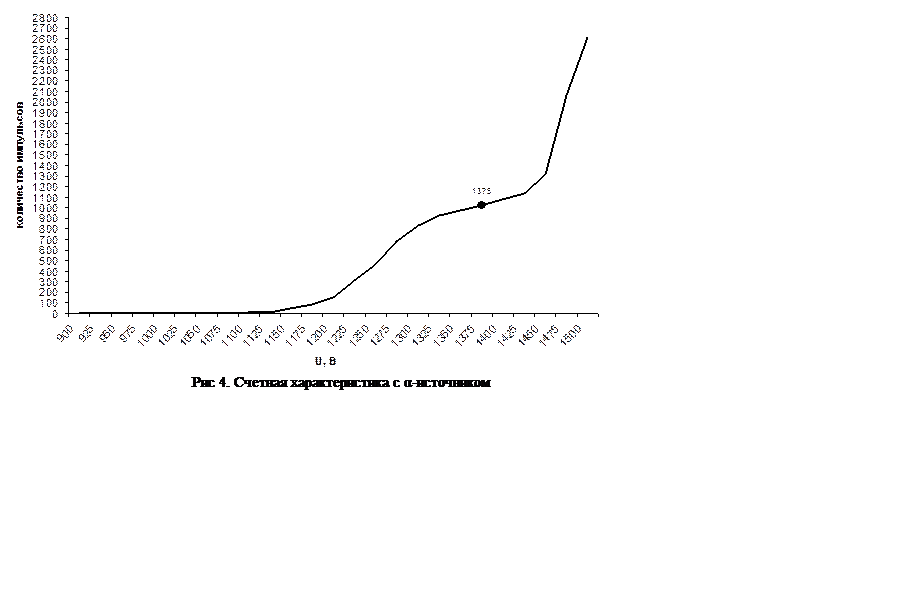 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.