Теневой метод изучения газового промежутка. Сверхзвуковой газовый поток. Сопло Лаваля

1.Введение

Оптика находит широчайшее применение в различных науках, являясь подспорьем и неотъемлемой частью гигантского числа экспериментов. Большую долю информации человек всегда воспринимал глазами и оптические системы ,помогающие обозреть какие-либо физические явления не доступные невооруженному глазу, очень сильно помогают ученым. С их помощью можно много быстрее осознать какие-либо истины, установить закономерности и в конце концов просто представить себе картину физического явления.

Газовая динамика никак не может обойтись без оптики, ведь очень большое количество задач с газовыми потоками расцениваются ,как теоретически нерасчетные. Но используя, например, приборы теневого метода изучения газовых промежутков, можно качественно рассмотреть изменение плотности потоков газа и узнать, как же на практике распространяются набегающие фронты газового потока и многое другое. При помощи этих приборов можно попросту напрямую наблюдать физический процесс. Это во многом облегчает людям жизнь, а зачастую это единственный метод, с помощью которого можно получить необходимую информацию. Ведь далеко не всегда в физике можно все рассчитать в теории, результаты экспериментов всегда будут не менее важны.

2.Теоретическая часть.

2.1 Теневой метод изучения газового промежутка.

Теневой метод широко применяется в современном аэрофизическом эксперименте для визуализации и получения количественных данных о полях плотности в исследуемых течениях. К наиболее существенным достоинствам этого метода относятся :

1.  Панорамность  информации сразу по всему полю исследуемого объекта.

2.  Их бесконтактность, т.е. получение информации без внесения каких-либо датчиков и искажений в исследуемый поток.

3.  Возможность получения “мгновенных“ по сравнению с характерным временем исследуемого процесса фотоснимков. Например использование в качестве света рубинового лазера с модулированной добротностью дает информацию за время  с.

В основе теневых методов лежит связь показателя преломления газа в точке с его плотностью :

Где  – показатель преломления ,  – плотность газа ,  – постоянная для данного газа величина (постоянная Гладсона – Дейля)

Сущность теневого метода заключается в следующем :

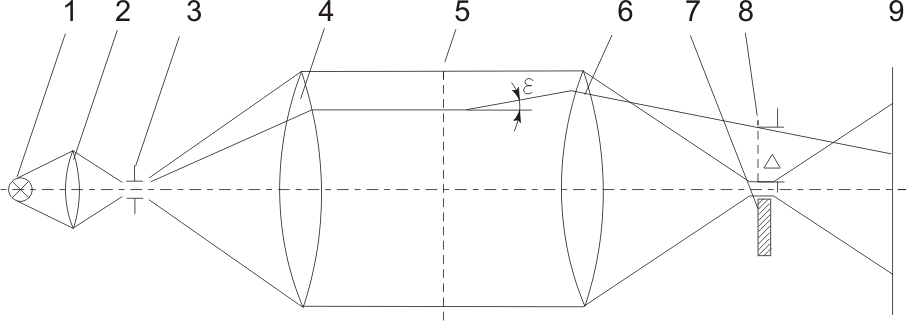
Рис. 1 Принципиальная схема :

1 – источник света; 2- конденсор; 3 – щель; 4,6 – длиннофокусные объективы; 5 – теневая картина неоднородности;        7 – диафрагма; 8 – плоскость ; 9 – экран;

Длиннофокусные объективы 4 и 6 создаю в плоскости 8 изображение ярко освещенной щели 3. В этой же плоскости установлена диафрагма 7 (нож Фуко), которая при перекрывании изображения щели вызывает по всему полю равномерное ослабление яркости на экране 9.

Если в поле параллельного хода лучей ввести оптическую неоднородность , отклонение лучей в ней вызовет перераспределение освещенности на экране 9. В этом случае на экране будет наблюдаться теневая картина неоднородности 5.

Угол отклонения луча Е в данной точке неоднородности определяется как отношение величины δ линейного перемещения ножа до момента перекрывания отклоненного луча к величине fзаданного фокусного расстояния объектива 6:

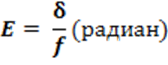
Угол отклонения луча Е связан с градиентом показателя преломления оптической неоднородности следующим соотношением

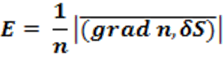
Где - путь лучей в оптической неоднородности ,  – местное значение показателя преломления.

После интегрирования получают поле показателя преломления в исследуемой среде, которая в свою очередь зависит от плотности потока. Значит можно говорить о поле показателя плотности в среде.

2.2 Сверхзвуковой газовый поток. Сопло Лаваля.

Сверхзвуковой поток в данной курсовой работе получался применением сопла Лаваля.

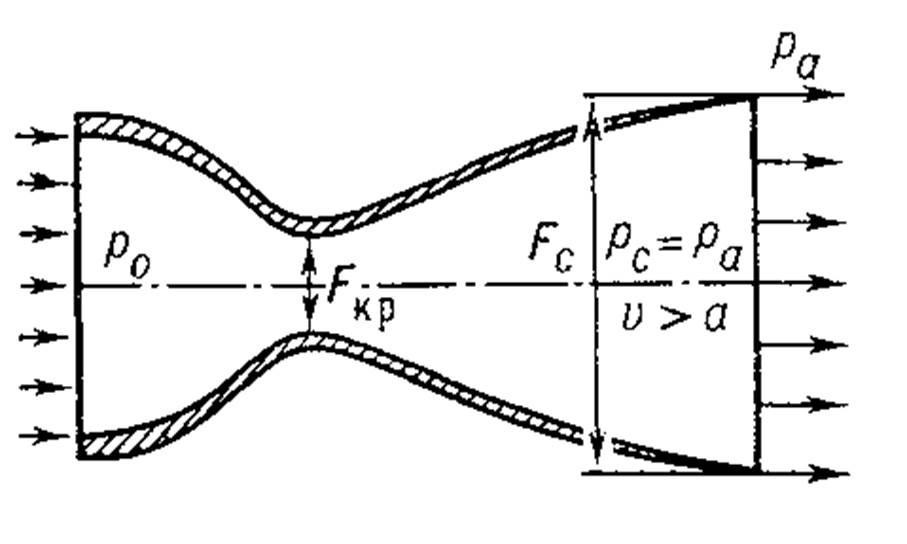
Рис.2 Сопло Лаваля

Из уравнения неразрывности и уравнения Бернулли в дифференциальной форме можно записать равенство :

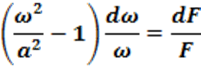
Где  – скорость газового потока , – скорость звука ,  – площадь сечения сопла.

1.  ω<a →  < 0 (сопло сужается)

2.  ω=a →  = 0 (критическое сечение)

3.  ω<a →  < 0 (расширение сопла)

Значит у этого сопла наблюдается три режима : дозвуковой , критический и сверхзвуковой.

Преобразовывая формулу отношения площади сечения к критической площади получим :

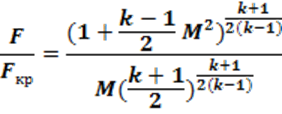
Это функция которая зависит только от M(маха) – отношения скорости газового потока к скорости звука. Одинаковым значениям отношения площадей соответствует по два значения, соответственно в дозвуковом и сверхзвуковом режимах сопла. Это значит что каждому сечению сопла соответствует свое значение маха, но так же каждому сечению соответствует своя температура, давление и плотность газа. Неизменным остается отношение :

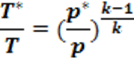
Где  – температура торможения ,  - изменение полного давления.