 |
Было произведено измерение числа импульсов при интервалах 500 и 5 мс, измерено среднее квадратичное отклонение (СО) и среднее квадратичное отклонение среднего (СОС). Полученные результаты представлены на рис 4.
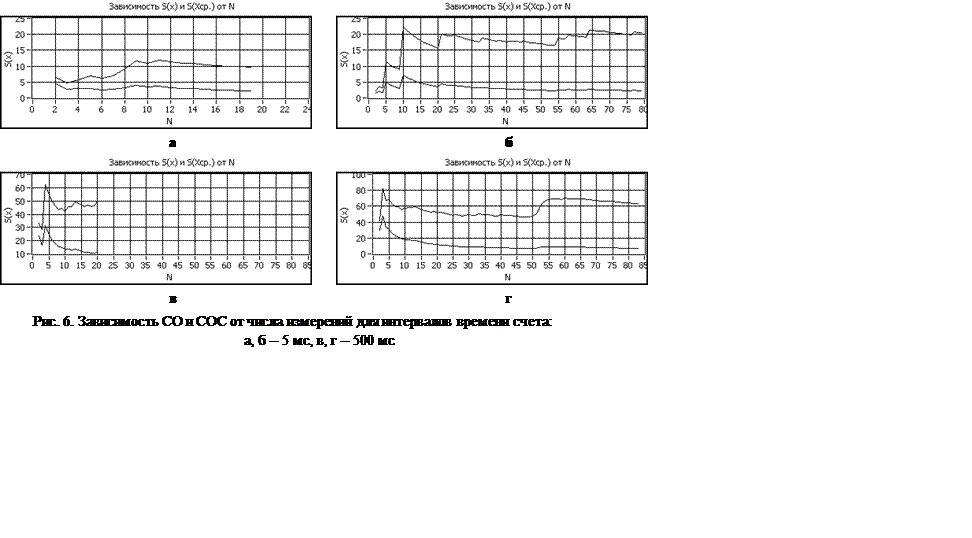 |
Таблица 1. значения ![]() ,
, ![]() ,
, ![]() при времени
счета 1 мс
при времени
счета 1 мс
|
ΔT, мс |
N |
|
|
|
|
|
1 |
10 |
9,60 |
1,30 |
0,0183 |
5,32 ∙ 10-4 |
|
50 |
12,30 |
0,77 |
0,0111 |
4,68 ∙ 10-3 |
|
|
100 |
10,79 |
0,27 |
0,0067 |
2,70 ∙ 10-3 |
|
|
150 |
10,85 |
0,37 |
0,0183 |
4,68 ∙ 10-3 |
|
|
200 |
10,55 |
0,34 |
0,0111 |
8,15∙ 10-3 |
Таблица
2. значения ![]() ,
, ![]() ,
, ![]() при 100 измерениях в выборке
при 100 измерениях в выборке
|
N |
№ |
ΔT, мс |
|
|
|
|
|
100 |
1 |
1 |
11,99 |
0,56 |
77886,60 |
7,56 ∙ 107 |
|
2 |
10 |
73,92 |
1,52 |
0,30 |
866,73 |
|
|
3 |
100 |
566,17 |
2,99 |
1,50 |
0,65 |
|
|
4 |
1000 |
8093,83 |
71,55 |
6,64 |
5,65 ∙ 1018 |
|
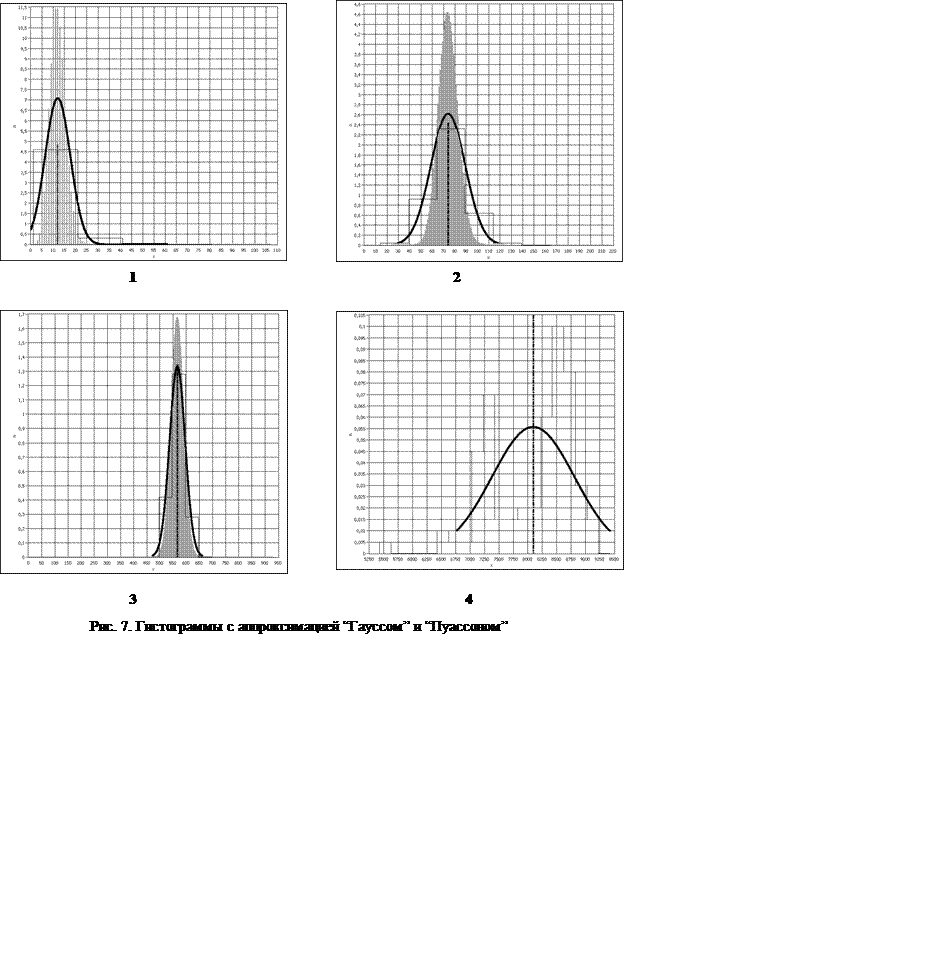
По данным таблицы 2 построены гистограммы, аппроксимируемые распределениями Гаусса и Пуассона. Данные гистограммы представлены на рисунке 7 (номерам гистограмм соответствуют номера в таблице 2).
 |
По
данным пункта 3.3 был произведен расчет активности рассматриваемого образца по
формуле: 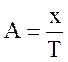 , где A – активность
образца, x – количество импульсов, зарегистрированных детектором
за время T.
, где A – активность
образца, x – количество импульсов, зарегистрированных детектором
за время T.
Ошибку
в полученный результат будет вносить преимущественно случайная погрешность
измерения количества регистрируемых импульсов, т.к. систематической
погрешностью, связанной с темновым током, пренебрегается из-за малости его
величины тока, а ошибка вносимая временем не учитывается по причине
программного считывания времени, вносящего малую ошибку в получаемые результаты
из-за значительной скорости АЦП. Исходя из этого, погрешность измерений
активности образца может быть рассчитана по формуле: 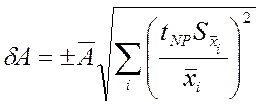
Таким
образом, активность образца равна: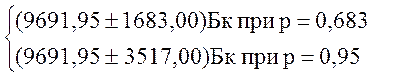
В результате выполнения работы цель – ознакомиться с методами обработки экспериментальных данных была достигнута. Выявлены следующие статистические закономерности: среднеквадратичное отклонение растет, а среднеквадратичное отклонение среднего убывает с увеличением количества проводимых измерений величины.
Активность исследуемого образца плутония - 239 составила:
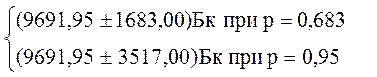 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.