Спектрофотометрия. Кислотно-основные равновесия, страница 4

Далее, логарифмируя с учетом того, что рН = — lg а_н+, полу­чаем итоговую формулу, позволяющую рассчитывать константу диссоциации одноосновной кислоты в буферном растворе.

lgK_a  =  lg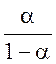 –  pH + lg f_- .

Определение константы диссоциации бромтимолового синего

В данной работе исследуется кислотно-основное равновесие, устанавливающееся в растворах 3,3 ́ – дибромсульфофталеина (бромтимолового синего, или БТС).

            В литературе приводится два типа формул, описывающих строение этого индикатора.

                           

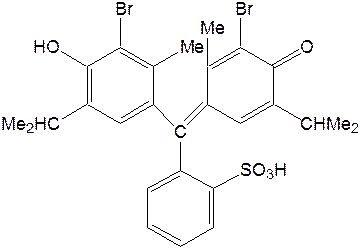
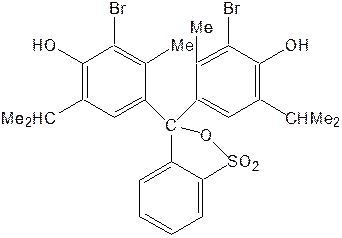
В условиях данной работы исследуется процесс диссоциации индикатора по второй ступени:

НА^– + Н₂О ↔ А^2– + Н₃О.

В случае достаточно разбавленных растворов константа диссоциации индикатора по второй ступени связана со степенью диссоциации α и с рН раствора соотношением:

lgK_a  =  lg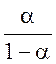 –  pH + lg f_- .

Значение α находится по формуле 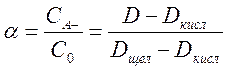. Коэффициенты активности каждого из анионов f_i–: .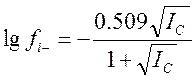

Зная для одного и того же раствора значения α, рН и f_i– можно рассчитать значение константы диссоциации K_a по второй ступени.

Таблица №1. Определение коэффициентов экстинкции протонированной и депротонированной форм БТС.

Форма индикатора	Конц. Индикатора С, М	Длина волны, λ, нм	Оптич. Плотность Dλ	Коэффициент экстинкции ε, М–1·см–1	εср ± σn
Протонир. НА–	5,13E-05	440(433)	0,859	16750,5	15221,38 ± 1891,224 (18072,576 ± 215,444)
	3,85E-05		0,619	16094
	2,56E-05		0,399	15561
	3,21E-05		0,160	12480
Депротонир. А2–	2,56E-05	620(617)	1,041	40599	31872,75 ± 8976,293 (43563,398 ± 770,556)
	3,21E-05		0,460	35880
	6,41E-06		0,201	31356
	3,21E-06		0,063	19656

Построили график зависимости D_λ от С.

Протонированная форма

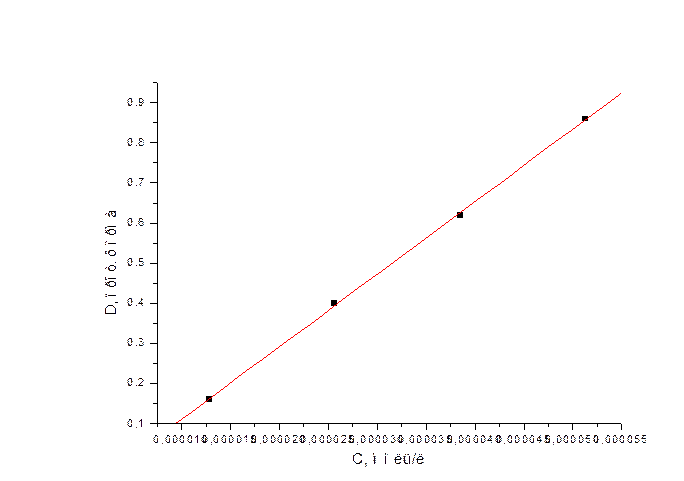
Депротонированная форма

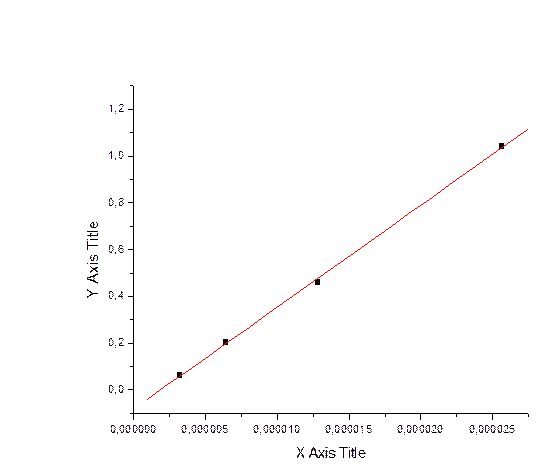
Обработали спектры растворов №3, 5, 9, 10.

Нашли параметры изобестической точки: λ = 510 нм, ε = D/ С = 0,11/ 2,56E-05 = 4296,875.

Номер раствора	рН	Ic, М	lgf	Dλ			αλ			lgα/(1-α)			lgKα			Kα
				λ1 (440)	λ2 (620)	λ3 (320)	λ1	λ2	λ3	λ1	λ2	λ3	λ1	λ2	λ3	λ1	λ2	λ3
3	3,3	0,01	-0,046	0,399	-0,02	0,166
5	10,7	0,01	-0,185	0,022	1,041	0,359
9	6,86	0,01		0,265	0,322	0,238	0,355	0,322	0,373	-0,259	-0,323	-0,226	-7,258	-7,322	-7,225	5,52·10–8	4,76·10–8	5,96·10–8
10	7,3	0,01		0,220	0,580	0,281	0,475	0,566	0,596	-0,043	0,115	0,169	-7,482	-7,324	-7,27	3,30·10–8	4,74·10–8	5,37·10–8
Среднее значение													-7,314			4,94·10–8
Погрешность определения													0,090974			0,930·10–8