Спектр щелочных металлов. Многоэлектронные атомы. Одноэлектронное приближение с учетом кулоновского взаимодействия электронов

Лекция 2.

  Спектр щелочных металлов.

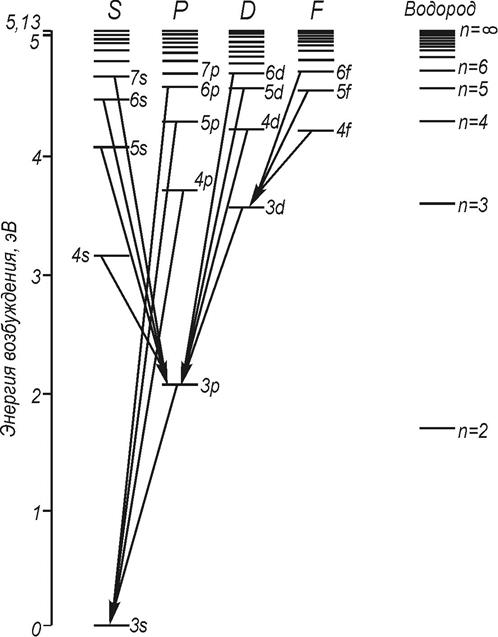
один 1s-электрон в верхней подоболочке, спектр существенно отличаются от спектра водорода (см. диаграмму):

снято вырождение по орбитальному моменту  внешнего электрона.

 энергия уровня зависит от  настолько сильно, что нельзя уже говорить о расщеплении уровня с данным n. Скорее, уровни с заданным  описываются водородоподобно (см. раздел 1.1) с эффективным квантовым числом n*.

каждый из энергетических уровней, кроме S термов, расщеплен на два за счет спин-орбитального взаимодействия. Значение J равно J = L ± 1/2 при L  0 и J = 1/2 при L = 0. Правила отбора аналогичны приведенным выше.

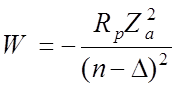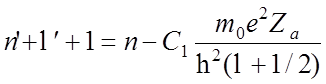,      =n -

 

Поправка Ридберга  не зависит от   n

Многоэлектронные атомы. Одноэлектронное приближение с учетом кулоновского взаимодействия электронов. Метод самосогласованного поля. Уравнение Хартри

Более близкие к истинным одноэлектронные приближения получаются с помощью метода ССП. Действие полей всех остальных электронов на данный электрон заменяется здесь средним полем, эффект которого приближенно равен суммарному действию остальных электронов. Взаимодействие электрона с полем при этом зависит только от координат рассматриваемого электрона.

Следовательно, задача ССП сводиться к определению одноэлектронных состояний многоэлектронного атома.

С учетом найденного выше нулевого приближения гамильтониан многоэлектронного атома запишем в виде

. 

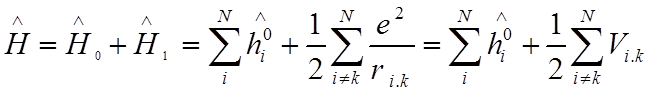Найдем энергии основного состояния атома из условия минимума вариации функционала энергии (Давыдов с.374; Давтян , 225, Ландау с. 81)

,

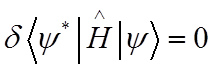                          (6)

y - некоторая пробная ВФ, удовлетворяющая условию нормировки. Минимальные значения интеграла будет энергией основного состояния.

Пусть это будет функция Хартри (3).

 

 

Подставив ее в (6), получим систему уравнений (Хартри (D.R.Hartree) 1928 г.)

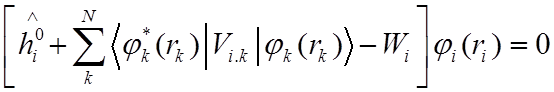                                   (7)

Сумма интегралов 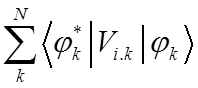 определяет в координате потенциал кулоновского воздействия на i-й электрон остальных (N-1) электронов.

Решается система (7) методом итераций.

0-я итерация: вычисляем кулоновский потенциал  для i-го электрона с водородоподобными функциями (из таблицы)

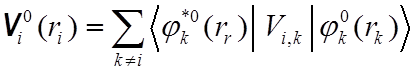.                                   (8)

Подставляем найденные значения в систему (7) и находим .

1-я итерация: используем  для вычисления потенциалов первой итерации

,

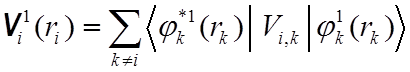которые используем для вычисления следующего набора орбиталей .  

Если процесс сходится, то можно получить самосогласованное поле Хартри (ВФ с полем согласованы) в форме (8). Усредняя по направлениям , можно привести его к  центрально-симметричным виду. Это  позволяет разделить переменные УШ. Решения соответствующих УШ дают одноэлектронные состояния, аналогичные рассмотренным выше в  приближении независимых электронов. Одноэлектронный гамильтониан ССП Хартри отличается от водородоподобного на .

Одноэлектронность. Таким образом, метод ССП Хартри также приводит к одноэлектронному приближению, но уже с учетом межэлектронного кулоновского взаимодействия. Найденные электронные состояния и соответствующие орбитали (уже не водородоподобные!) характеризуются, как и в атоме водорода, тремя квантовыми числами: ,  и .

Энергия электрона в атоме будет определяться также формулой Бора, но с зарядом Z_эфф.

Однако в методе Хартри также не учитывает принцип Паули, что приводит к неправильному распределению электронов

Метод самосогласованного поля с учетом принципа Паули. Уравнение Хартри-Фока

Определяющим параметром принципа Паули является спин электрона (обозначается буквой s), открытый Гоулдсмиттом и Улунбеком (1925 г).

Принцип Паули

Электронная ВФ системы из нескольких электронов должна быть антисимметричной (менять знак) относительно обмена положениями и спинами пары из любых двух электронов i и k:

.

Следствие. Никакие два электрона не могут быть в одном и том же квантовом состоянии (принцип исключения).

Паули сформулировал принцип, анализируя отсутствующие двухэлектронные  состояниям с одинаковыми квантовыми числами в спектрах атомов. Например, у атома гелия отсутствует состояние 1³S.

ВФ с учетом спина. Спин-орбиталь

Проекция спина.  новое квантовое  число  m_s

m_s = + ½  «спин вверх» иногда обозначается буквой α,

m_s = – ½  «спин вниз» иногда обозначается буквой β                  (9)

Следовательно, одноэлектронные состояния электрона в атоме описываются четырьмя квантовыми числами , ,  и .

ВФ спиновых состояний. В соответствие  с (9) спиновое состояние электрона в атоме можно описать двухразмерным вектором, называемый спинором, проекции, которого равны

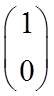  и    .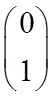

Поскольку гамильтониан в первом приближении не содержит спиновых переменных и поэтому его воздействие не влияет на спиновые составляющие  ВФ. Следовательно ВФ электрона с учетом спинового состояния может быть записана в виде произведения орбитали и спинора (Ландау, 268):

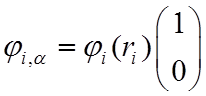= – «спин вверх», α-состояние,

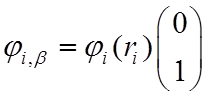=– «спин вниз», β-состояние.          (10)

Волновые функции (10) называют спин-орбиталями. Заметим, что спин-орбитали (10) ортогональны, действительно

.

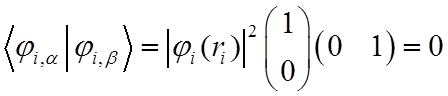Сконструируем антисимметричную ВФ для простейшей системы из двух невзаимодействующих электронов (атом Не).