Спектр щелочных металлов. Многоэлектронные атомы. Одноэлектронное приближение с учетом кулоновского взаимодействия электронов, страница 2

Предполагая независимость электронов, составим сначала функцию   в виде произведения спин-орбиталей (10) отдельных электронов

.

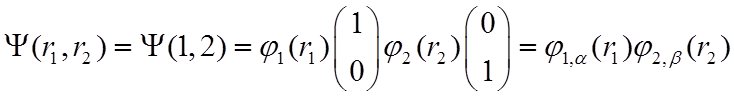Перестановочная симметрия такой функции не определена, то есть может быть произвольной.

Антисимметричное решение УШ, удовлетворяющее принципу Паули, может быть создано в виде следующей линейной комбинации

.

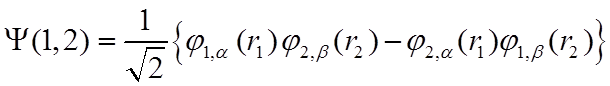Детерминант Слейтера. С математической точки зрения, вид этой функции есть детерминант:

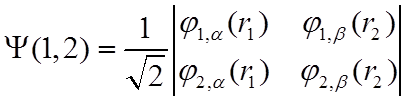
                              (11)

Перестановке пары электронов соответствует перестановка столбцов или строк детерминанта, при которой, как известно, изменяется его знак, что удовлетворяет требованию перестановочной антисимметрии ВФ.

Антисимметричную спин-орбиталь для системы из N электронов можно также представить в виде детерминанта из спин-орбиталей (Давтян, §19, Герцберг, ММ, 342)

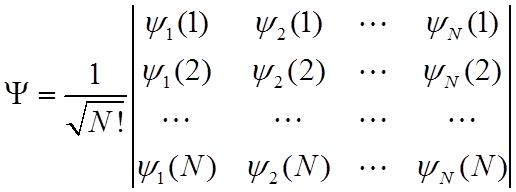,                     (12)

называемого детерминантом Слейтера.  Здесь использовано обозначение i-ой спин-орбитали для j-го электрона в виде , где  – координатная, а  – спиновая часть ВФ;  – совокупность координат j-го электрона.

Одноэлектронное уравнение Хартри –Фока

Используя функцию (12) в качестве пробной в уравнении

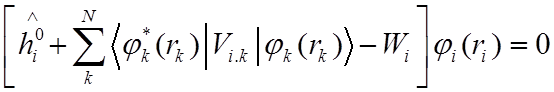                                   (7)

(7), можно получить систему из N уравнений, называемых уравнениями Хартри –Фока

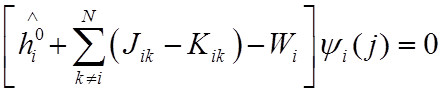,      i =1,2,…N,                          (7*)

,

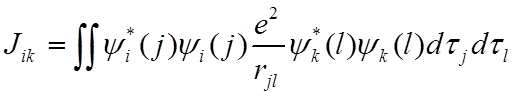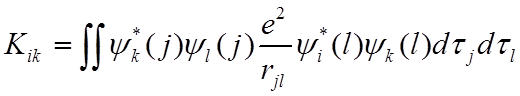
впервые рассмотренные ленинградским физиком В.А.Фоком (1930 г.).

Интегралы  носят название – кулоновских интегралов.

Интегралы  – называется обменными интегралами

Решается УХФ также методом последовательного приближения. В качестве пробной функции используют решения соответствующих уравнений Хартри. Оба  интегро-дифференциальных уравнения ССП решаются только численно.

Вывод

Изложен метод, позволяющий использовать одноэлектронное приближение при изучении физики и химии многоэлектронного атома. Рассмотренный метод используется и является эффективным также при изучении свойств молекул.

1.2.  Атомы с двумя и более электронами в верхней оболочке

Атом гелия:  Решим задачу методом возмущений

в нулевом приближении   ,

где    .

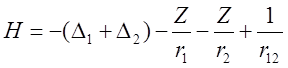 =H₀ + H₁

По принципу Паули для частиц с полуцелым спином  осуществляются состояния лишь с антисимметричными полными волновыми функциями.

                     

                     

                     

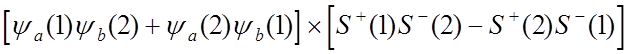
где    и    -  спиновые волновые функции электронов ;     .

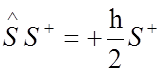          В соответствии со стационарной теорией возмущений, поправка к энергии определяется выражением:

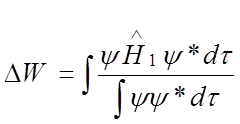   ,     где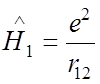     

Получаемую поправку к энергии можно представить в виде (переобозначим 1,2 → a,b более детально см. Матвеев §52)

      при   ,

      при   (a = b),

Знак + относится к синглетному состоянию (S=0, парагелий), а – к триплетному (S=1, ортогелий)

где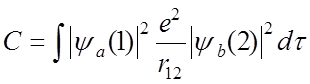       

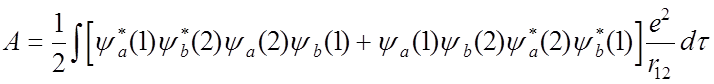
Полная энергия атома гелия равна:

           при     a = b         

                          

Знак + относится к синглетному состоянию (S=0, парагелий), а – к триплетному (S=1, ортогелий)

Итак,  проведем сравнение точности двух методов решения задачи: метод возмущений и вариационный метод (Ландау §69)

·  В методе возмущений используются известные волновые функции, полученные для атома водорода. Нулевое приближение дает невозмущенное значение энергии связи, равное удвоенному (два электрона) основному уровню водородоподобного иона с зарядом Z :

·   

·  2 W _a =  2 (- Z² / 2) = - Z²  =  27.2*4 = 108,8 эв.

·   

Поправка С равна:

С=5/8Z,

Следовательно полная энергия  для гелия  (Z=2)  :

W= - Z²  + 5/8 Z =  11/4 =2,75* 27.2 =  74.8 эв

Реальное значение W = 2.90* 27.2 = 78,9 эв

С+А =29.8 эв

2А = 0.75 эв

·  Проделаем то же самое с помощью вариационного принципа  аппроксимируя волновую функцию в виде произведения двух водородоподобных функций с некоторым эффективным  зарядом ядра Z_эфф . При этом H входит заряд Z

·   

H = -Z/r₁ –Z/r₂ + 1/r₁₂

Получим , что выражение 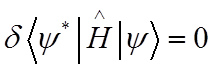 можно представить в виде

,

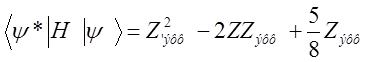которое имеет минимум , как функция от Z_{’эфф ,} при

Z _{эфф =} Z – 5/16

Соответствующее значение энергии:

 W = -Z² _эфф = -(Z– 5/16)² = 2.85

Диаграмма Гротриана для атома гелия

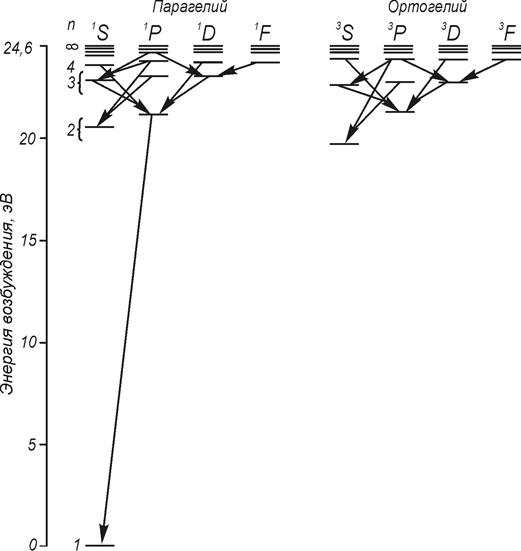
Оценка из диаграммы (n=2) для 2А~0.75 эВ.

 Если один электрон возбужден , то можно использовать схему решения, аналогичную применявшейся для атомов щелочных металлов. 

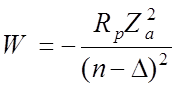 где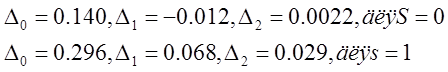

Таким образом, наличие электростатического взаимодействия между электронами  ,  а также учет идентичности электронов и требований симметрии волновых функций приводят: к смещению энергетических уровней, причем значение смещения, определяемое, в основном, величиной поправки С, зависит от орбитального момента   электронов;  к расщеплению энергетических уровней в зависимости от ориентации их спинов. Следовательно, снимается вырождение по величине  L и  S.

Однако, энергия атома не зависит от взаимной ориентации   и   т.е. остается вырождение по величине и направлению полного момента  .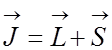

Очевидно, что данные выводы применимы и к атомам со многими электронами.