Релаксационные процессы в газах. Вращательная релаксация. Колебательная релаксация

Лекция №10

 Релаксационные процессы в газах

При рассмотрении химических реакции, которые происходят в результате протекания большого числа различных элементарных реакций, часть из которых подчас мало изучено, необходимо уметь выделить основополагающие реакции. Здесь может быть полезным установление «иерархической» шкалы времен – определение характерных времен элементарных реакции в сравнении с характерным временным масштабом задачи. Для элементарных реакций таким временем является время релаксации.

Для возбуждения каждой из степеней свобод (под которыми помимо поступательной, вращательной и колебательной степеней свободы будем иметь в виду и химические превращения) и установления термодинамического равновесия требуется некоторое время, масштабом которого служит так называемое время релаксации. Времена релаксации для возбуждения различных степеней свободы сильно различаются, поэтому возможны такие условия, когда термодинамическое равновесие устанавливается не во всех, а только в части степеней свободы. Скорее всего, равновесие устанавливается в поступательных степенях свободы и обычно наступает после нескольких столкновений   (~ 2-3) с частицами близкими по массе. Время установления Максвелловского распределения по скоростям имеет порядок среднего времени между газодинамическим столкновением 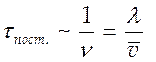;  - частота столкновений,  - средняя длина свободного пробега,  - средняя скорость. Для воздуха при нормальных условиях с. Обычно  - характерного времени, на котором заметно меняются параметры задачи (плотность, энергия) и поэтому можно в каждый момент времени приписать газу «поступательную» температуру – величину, характеризующую среднюю кинетическую энергию поступательного движения частиц. В состоянии неполного термодинамического равновесия, когда говорят о термодинамических равновесных степенях свободы, имеют в виду, что распределение энергии (и концентраций соответствующих компонент газовой смеси) в этих степенях свободы находятся в равновесии с «поступательной» температурой газа. Величины же, соответствующие неравновесным степеням свободы (распределение энергии и концентрации соответствующих частиц) могут быть произвольными и определяются не просто температурой, плотностью и элементным составом газа, как при термодинамическом равновесии, но и еще кинетикой физико-химических процессов, приводящих к установлению равновесия в данных степенях свободы. Времена релаксации для установления равновесия в различных степенях свободы часто сильно различаются. Если при данных  и  переходить от быстрых к более медленным релаксационным процессам то цепочка будет выглядеть: поступательные степени свободы; вращение молекул, колебания молекул; диссоциация и химические реакции; электронное возбуждение и ионизация.

Благодаря весьма большому различию во временах релаксации, каждый из релаксационных процессов можно изучать в отдельности, выделяя его из остальных и предполагая, что в легко возбуждаемых степенях свободы равновесие наступило, а более медленные релаксационные процессы вообще не идут на протяжении рассматриваемых времен.

Все релаксационные процессы обладают некоторыми общими чертами, независимо от их природы. А именно, приближение состояния термодинамического равновесия в данной степени свободы происходит асимптотически по экспоненциальному закону. Если, например, говорить о числе частиц, участвующих в каком либо химическом превращении, то при заданных  и  (и элементном составе) газа можно записать:

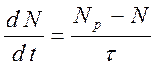                                                                               (10.1),

где  - равновесное число частиц, а  - время, характеризующее переход к равновесному состоянию.

Решение уравнения (10.1); с начальным условием  есть:

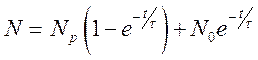                                                                          (10.2)

и видно, что  - есть время релаксации данного процесса (при  функция меняется в  раз).

В общем виде уравнение кинетики может быть представлено как

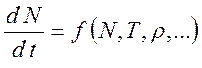                                                                                  (10.3),

тогда уравнение (10.1) есть первое приближение, если функцию в правой части (10.3) представить в виде разложения по малому отклонению от равновесия .

Рассмотрим релаксационные процессы в газе, состоящем из двухатомных молекул. Уровень энергии двухатомной молекулы складывается из трех независимых частей – электронной энергии (в которую включают так же и энергию Кулоновского взаимодействия ядер), энергии колебания ядер внутри молекул и вращательной энергии.

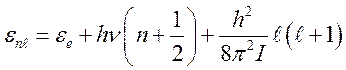                                                              (10.4).

Здесь  - электронная энергия;  - колебательный квант;  - колебательное квантовое число;  - вращательное квантовое число.  - момент инерции молекулы (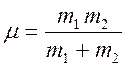;  - равновесное значение расстояния между ядрами).

Статистическая сумма молекулы соответственно запишется

                                                                                    (10.5),

где

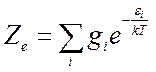          ;                                                                                        (10.6)

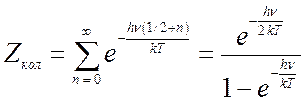                                                                    (10.7),

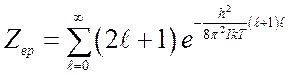                                                                      (10.8).

Вращательная релаксация.

Энергия вращательного кванта, выраженная в градусах 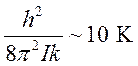, то уже

при комнатных температурах будем иметь 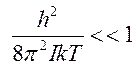 и в (10.8) суммирование можно заменить интегрированием.

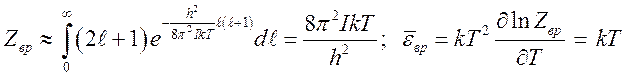                      (10.9).

Отсюда видно, что даже при комнатных температурах, а тем более при более высоких температурах, квантовые эффекты вращении молекул не проявляются и молекулу можно рассматривать как классический ротатор со средне энергией . Поэтому молекулы при столкновениях интенсивно обмениваются поступательной и вращательной энергией с характерным временем, которое можно оценить следующим образом: , откуда

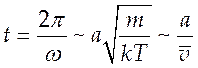                                                                          (10.10),

где a - размер молекулы, - средняя тепловая скорость.