




Под рекомбинацией обычно подразумеваются такие столкновения носителей заряда противоположного знака, двигающихся в газе, которые приводят к их взаимной нейтрализации. Если оба носителя — ионы, то процесс называется ионной рекомбинацией, если же один из них электрон, а другой — положительный ион, то говорят об электрон-ионной рекомбинации [5, 8, 10].
Рекомбинация обычно характеризуется коэффициентом рекомбинации ![]() , определяемым как число
, определяемым как число ![]() актов рекомбинации в единице объема за
единицу времени, деленное на произведение плотности носителей заряда
актов рекомбинации в единице объема за
единицу времени, деленное на произведение плотности носителей заряда
![]() (9.1)
(9.1)
В простой двухкомпонентной системе обычно выполняется условие
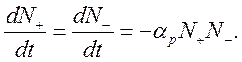 (9.2)
(9.2)
Коэффициент рекомбинации связан с сечением рекомбинации ![]() соотношением
соотношением
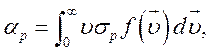
которое
приближенно можно записать в виде ![]() , где
, где ![]() — средняя тепловая скорость.
— средняя тепловая скорость.
Предположив ![]() ,
, ![]() , и что
при t = 0
, и что
при t = 0 ![]() получим
получим
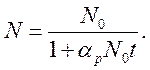 (9.3)
(9.3)
Если в системе имеется источник ионизации Q и начальная плотность ![]() , то
, то
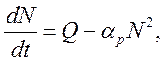 (9.4)
(9.4)
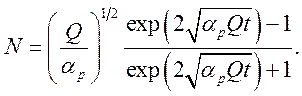 (9.5)
(9.5)
Плотность ионов возрастает с нуля при t = 0 до равновесного значения
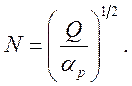
Когда рекомбинируют две частицы, их полная внутренняя энергия должна в результате реакции уменьшиться. В случае атомарных ионов такое уменьшение энергии равно разности между энергией ионизации и сродством электрона при образовании отрицательного иона. При электрон-ионной рекомбинации должна выделиться энергия ионизации получаемого нейтрального атома.
В силу требования сохранения импульса и момента импульса системы двух частиц переход энергии связи в кинетическую энергию рекомбинирующих частиц практически невозможен. Поэтому рекомбинация может проходить в следующих случаях: в присутствии третьей частицы, уносящей энергию, при излучении фотона или сопровождаться диссоциацией при рекомбинации молекулы.
Оценим скорость рекомбинации с участием электронов
![]()
![]() . (9.6)
. (9.6)
В соответствии с простейшей теорией, предложенной Томсоном, две частицы могут соединиться в том случае, если их полная относительная энергия станет отрицательной, т.е.
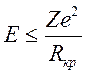 (9.7)
(9.7)
где Е — кинетическая энергия.
При столкновении
двух частиц это невозможно. Однако если два электрона сталкиваются между собой
на расстоянии ![]() от иона и энергия одного из
электронов после столкновения удовлетворяет условию (9.7), то он может быть
захвачен ионом.
от иона и энергия одного из
электронов после столкновения удовлетворяет условию (9.7), то он может быть
захвачен ионом.
Полное число столкновений электронов с другими электронами равно
![]() , (9.8)
, (9.8)
где ![]() —
средняя частота столкновений электронов. Тогда количество рекомбинирующих положительных
ионов определяется произведением
—
средняя частота столкновений электронов. Тогда количество рекомбинирующих положительных
ионов определяется произведением ![]() на вероятность
нахождения в этот момент положительного иона на критическом расстоянии
на вероятность
нахождения в этот момент положительного иона на критическом расстоянии ![]() , т.е.
, т.е.
![]() (9.9)
(9.9)
В единице объема в единицу времени с учетом (9.8) и (9.9) число актов рекомбинации равно
![]() (9.10)
(9.10)
Здесь
предполагается, что ![]() — сечение столкновения
электронов, при котором одной из частиц передается энергия порядка средней
кинетической энергии электронов Е, для того чтобы для второй выполнилось
условие (9.7).
— сечение столкновения
электронов, при котором одной из частиц передается энергия порядка средней
кинетической энергии электронов Е, для того чтобы для второй выполнилось
условие (9.7).
Учитывая, что ![]() , и если считать сечение передачи энергии
кулоновским
, и если считать сечение передачи энергии
кулоновским ![]() получим
получим
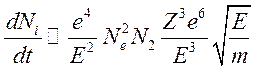 ,
,
т.е.
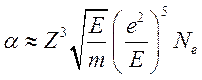 (9.11)
(9.11)
Точное выражение
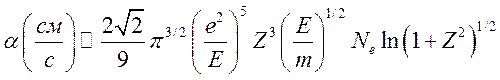 (9.12)
(9.12)
Определим сечение фоторекомбинации медленного электрона и иона с образованием сильно возбужденного атома. Поскольку энергия излучаемого фотона много меньше энергии связи электрона в атоме, то воспользуемся классической теорией тормозного излучения.
Интенсивность дипольного излучения
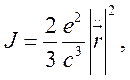 (9.13)
(9.13)
где ![]() — ускорение частицы.
— ускорение частицы.
Траектория, дающая основной вклад в рекомбинацию, сильно искривлена.
Пусть ![]() — прицельный параметр и
— прицельный параметр и ![]() — расстояние наименьшего сближения,
в котором кинетическая энергия частицы равна
— расстояние наименьшего сближения,
в котором кинетическая энергия частицы равна
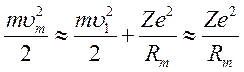 (9.14)
(9.14)
при рекомбинации
медленного электрона со средней энергией ![]() Из
закона сохранения импульса получим
Из
закона сохранения импульса получим
![]() (9.15)
(9.15)
Ускорение электрона в точке ![]() равно
равно
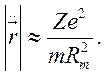 (9.16)
(9.16)
Подставляя (9.16) в (9.13), получим
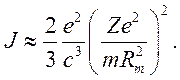 (9.17)
(9.17)
Вероятность столкновения с заданным прицельным параметром ![]() определяется сечением
определяется сечением
![]() (9.18)
(9.18)
Умножая J из (9.17) на время излучения ![]() , и с учетом (9.18), получим полную
излученную энергию
, и с учетом (9.18), получим полную
излученную энергию
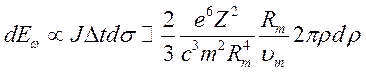 (9.19)
(9.19)
Используя (9.14) и (9.15), получим
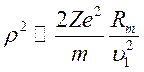
или
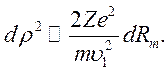 (9.20)
(9.20)
Основная излучаемая частота
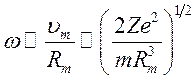 т.е.
т.е. 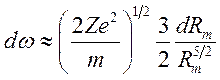 (9.21)
(9.21)
Учет (9.20) и (9.21) позволяет (9.19) переписать в виде
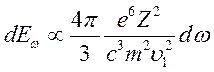 (9.22)
(9.22)
Излучаемая энергия связана с сечением рекомбинации ![]() также следующим соотношением:
также следующим соотношением:
![]() (9.23)
(9.23)
Сравнивая (9.22) и (9.23), получим
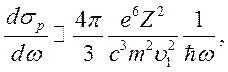
где должно выполняться соотношение
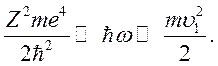
Учитывая, что ![]() , то
, то ![]() Или при
Или при
![]() получим
получим
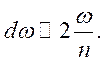 (9.24)
(9.24)
Здесь п — главное квантовое число уровня, на который попадает рекомбинирующий электрон.
Используя (9.24), получим окончательное выражение для сечения рекомбинации:
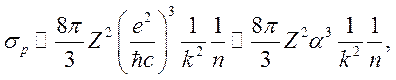 (9.25)
(9.25)
где ![]() .
.
Из формулы (9.25) видно, что рекомбинация может проходить на много
уровней, однако она максимальна при ![]() , т.е. при переходе
электрона в основное состояние атома. Полное сечение рекомбинации определяется
суммированием по п ряда
, т.е. при переходе
электрона в основное состояние атома. Полное сечение рекомбинации определяется
суммированием по п ряда ![]() , где
, где ![]() определяется условием, что при переходе на
него излучается фотон с энергией
определяется условием, что при переходе на
него излучается фотон с энергией 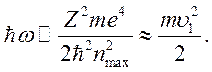
Полученное сечение рекомбинации называется формулой Крамерса.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.