ЛЕКЦИЯ
РАСТРОВЫЕ СПЕКТРАЛЬНЫЕ ПРИБОРЫ
С целью повышения светосилы классических спектральных приборов входная и выходная щели заменяются растрами – некоторая пространственная структура с определенным законом пропускания по плоскости и площадьюA=HS, где ширина растра S порядка высоты щели. Тем самым достигается увеличение светосилы в отношение S/s (s – ширина щели классического спектрального прибора). Изобретателем растра является Жирар (1960 г.). Выходной растр – это изображение входного.
Пропускание растра определяется двумерной функцией:
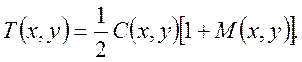 (1)
(1)
Здесь C(x,y) – это контурная функция, равная 1 внутри растра и 0 вне растра. M(x,y) – это некоторая функция определяющая пространственное пропускание растра. Свойства функций C(x,y) и M(x,y) даются соотношениями:
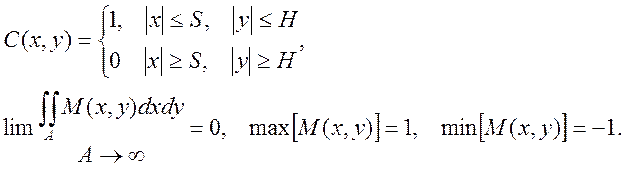 (2)
(2)
Распределение интенсивности за выходным растром при освещении входного монохроматическим излучением – аппаратная функция. Вид аппаратной функции определяется пропусканием света через смещенное на величину l изображение входного растра (l=Δλ*dl/dλ) и выходной растр:
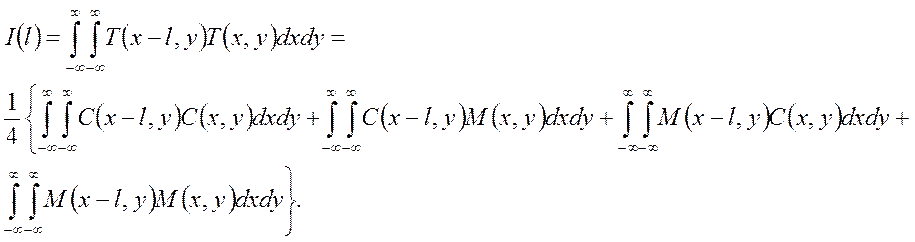 (3)
(3)
Первое слагаемое в (3) аналогично щелевой аппаратной функции спектрального прибора при равенстве выходной щели изображению входной щели. Второе и третье слагаемое - это почти ноль в силу свойства функции M(x,y). От последнего слагаемого ожидается узкая аппаратная функция. При этом суммарная аппаратная функция – это сумма широкой щелевой аппаратной функции, дающей некоторую засветку и узкой (как мы предположили) от четвертого слагаемого формулы (3).
Рассмотрим законы построения растра. Два растра при полном совмещении должны обеспечивать интегральное по площади пропускание около 1/2. При смещении растров должны наблюдаться равноотстоящие друг от друга муаровые полосы равной толщины (определенный класс растров), при этом интегральное пропускание (на единицу площади) в зоне перекрытия становиться равным 1/4. Полосы возникаю на краях растра и движутся к центру. Для одномерного растра функция M(x,y)=cos(f(x))*M(y). При этом четвертое слагаемое формулы (3) может быть записано следующим образом:
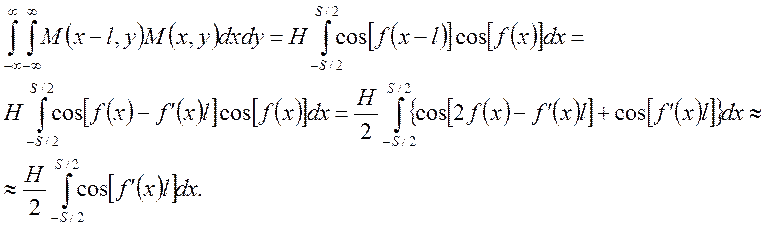 (4)
(4)
Огибающая пропускания двух смещенных растров – периодическая функция, равная cos(klx) (k – коэффициент пропорциональности, l – смещение двух растров, x – координата вдоль растра). l - имеет смысл пространственной частоты модуляции пропускания. Это означает f’(x) – линейная по x функция, т.е приращение фазы пропускания f(x) пропорционально координате х. Таким образом, для равноотстоящих муаровых полос f(x) квадратична по x. Смещение двух растров, при котором возникает две муаровые полосы, определяет разрешающую способность спектрального прибора. При увеличении смещения одного растра относительно другого должно расти число равно отстоящих муаровых полос, а пропускание должно оставаться равным 1/4.
Квадратичность f(x) можно также установить на основании следующих рассуждений. Пусть l – смещение двух одинаковых растров, k – будем обозначать номер прозрачного элемента растра, отсчитанный от середины растра, xk.- расстояние от центра растра до дальней границы прозрачного элемента, n – число светлых полос муара при смещении двух растров на расстояние l, b – ширина полосы муара. Светлая полоса муара будет наблюдаться при таком xk для одного растра, чтобы при смещении другого растра с прозрачным элементом xk совместился элемент xk+1 для другого растра. Следующая светлая полоса муара будет при условии совмещения xk и xk+2и так далее. Если наблюдается n светлых полос, то выполняется соотношение:
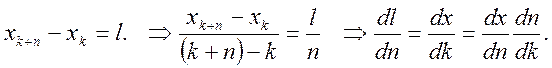 (5)
(5)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.