Рассеяние фотона на атоме

 

Рассеяние фотона на атоме

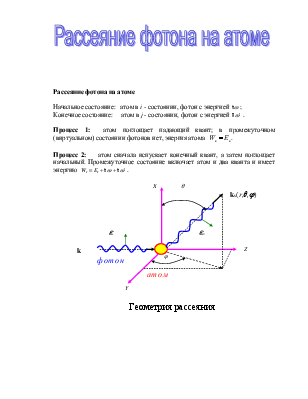
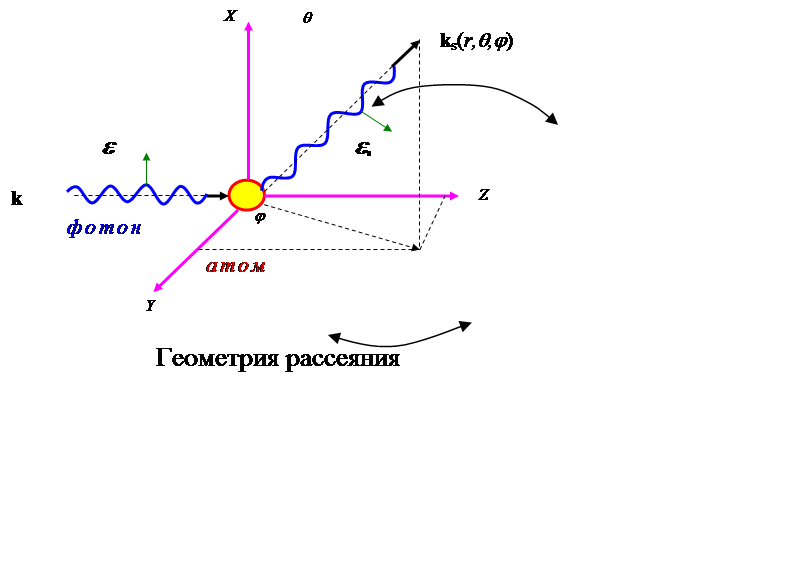
Начальное состояние:   атом в i - состоянии, фотон с энергией ;

Конечное состояние:     атом в j - состоянии, фотон с энергией .

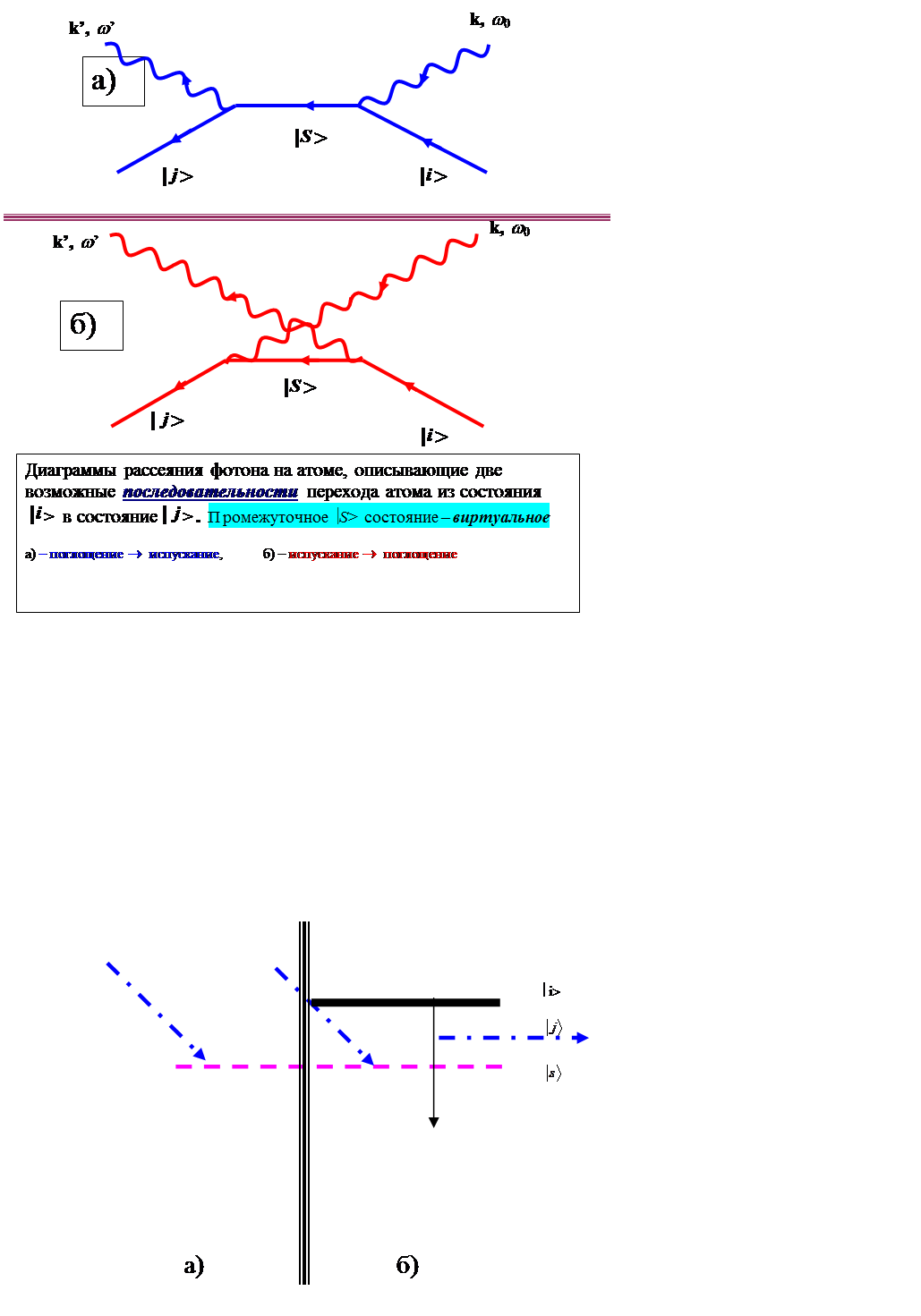
Процесс 1:  атом поглощает падающий квант; в промежуточном (виртуальном) состоянии фотонов нет, энергия атома  .

Процесс 2:    атом сначала испускает конечный квант, а затем поглощает начальный. Промежуточное состояние включает атом и два кванта и имеет энергию  .

 

 

             

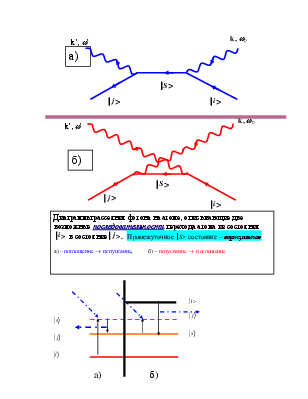
          При облучении среды наблюдается рассеяние света, длина которого содержит различные компоненты:

·  совпадающие с длиной волны падающего света (релеевское рассеяние на атомах), ;

·  отличающиеся от падающего на величину энергии кванта, характеризующего переходы в атоме :    - стоксова и   - антистоксова компоненты.

          Вероятность процесса

,

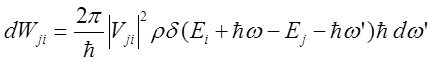где  - плотность конечных состояний

.

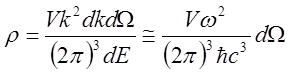          Матричный элемент процесса определяется вторым порядком теории возмущений:

.

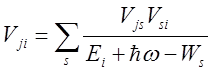          Дипольное взаимодействие:

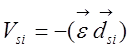   и   .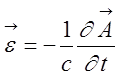

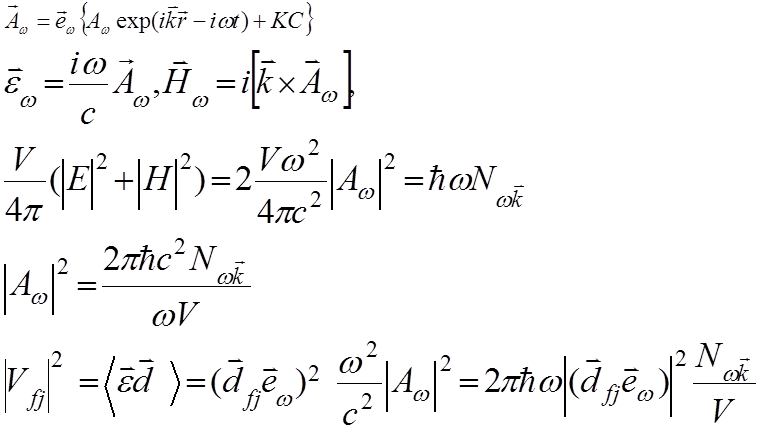
          Используя координатную зависимость компонент  , получим

,

.

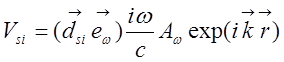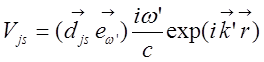          Учитывая два возможных канала рассеяния с   и   , для матричного элемента получим:

 ,

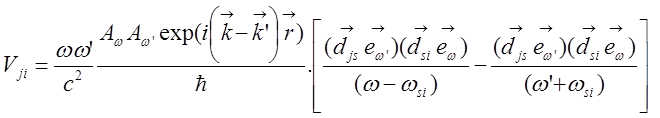где    ,         ,             

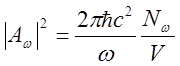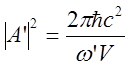
 т.е.   - рассеян один фотон.

          Для нахождения эффективного сечения рассеяния кванта в элемент угла  нужно вероятность  проинтегрировать по энергии  .

 ,

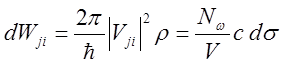здесь  - плотность потока налетающих фотонов.

 -

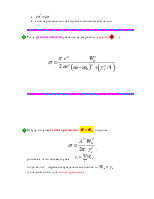
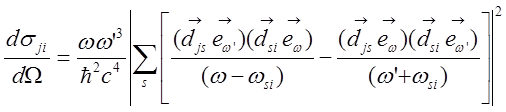дисперсионная формула Крамерса - Гейзенберга.

 (продолжение)

Из формулы Крамерса-Гейзенберга (ФКГ) видно, что при приближении к резонансу  сечение неограниченно растет, что противоречит эксперименту.

Необходимо учитывать естественную ширину уровней, т.е. сделать замену:

 .

 

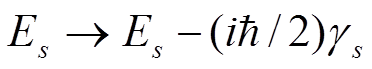Учитывая только «резонансный» член в ФКГ, получим дифференциальное сечение так называемой резонансной флуоресценции (Вайскопф,1931).

.

 

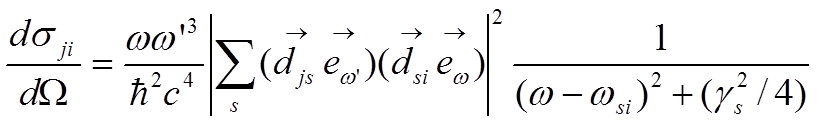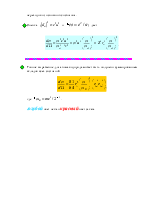
Полное резонансное поперечное сечение  получается интегрированием по телесному углу   и суммированием вкладов двух поляризаций

 .

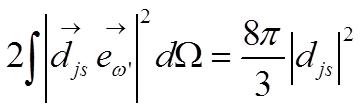Для сравнения с экспериментом необходимо учесть, что поток фотонов рассеивается на большом числе атомов. Сечение  усредняется по углам  . При равновероятном распределении , при этом среднее

значение   равно 1/3.

В результате получим сечение резонансной флуоресценции

.

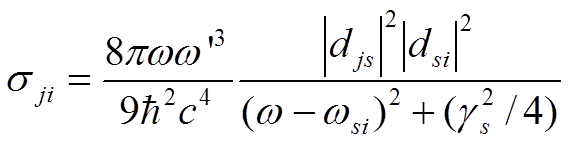Учитывая, что   ,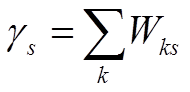 

 где                            ,

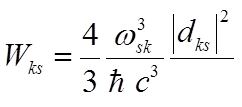определим сечение резонансной флуоресценции через вероятности переходов

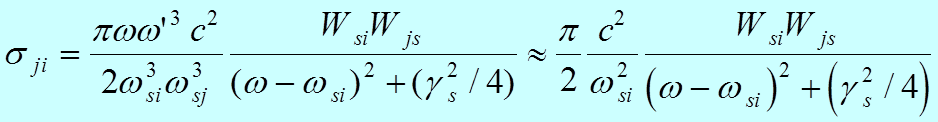
Здесь учтено, что вблизи резонанса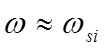  и   

Полное сечение неупругого рассеяния  фотона на атоме можно получить суммированием по всем конечным состояниям j , лежащим ниже s .

,

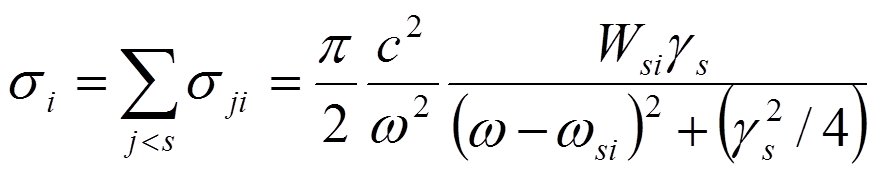 где                    .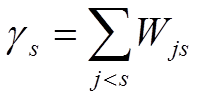

(Лоудон, глава 11, стр, ~393, ~413)

 

Условия задачи

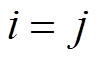·   (под действием фотона атом переходит лишь на промежуточный уровень)

·  .

·  атом первоначально находится в основном состоянии.

 

Тогда «резонансное» сечение будет равно (из формулы           )

,

 

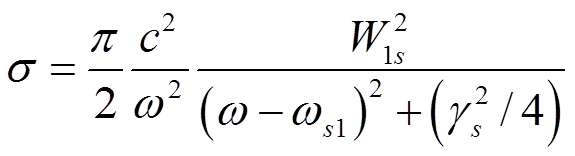Откуда в случае точного резонанса: 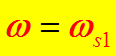 получим

,

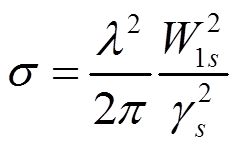учитывая, что в общем случае      ,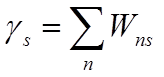

тогда, если s – первое возбужденное состояние, то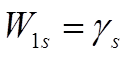

и, следовательно, для точного резонанса

 .

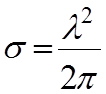~ 6 10^-10 см^-2, а вне резонанса ~7 10^-26 см^-2

 

Рассмотрим случай упругого рассеяния при 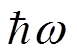 , много большем энергии первого возбужденного состояния атома.

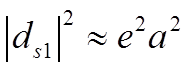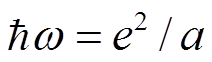дифференциальное сечение оценим, подставив в ФКГ значения  и , в результате получим

 .

 

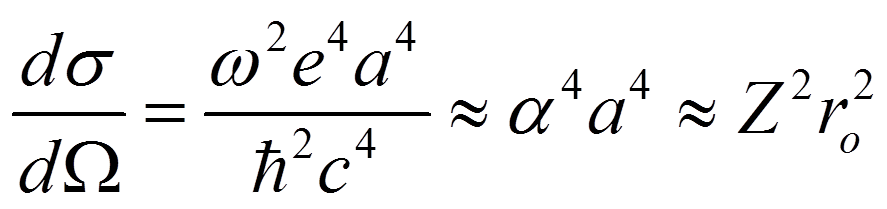Применение правила сумм осцилляторов

Точное выражение для дифференциального сечения с учетом влияния всех уровней, определяемое через правило сумм осцилляторов, в этом случае рано

.

 

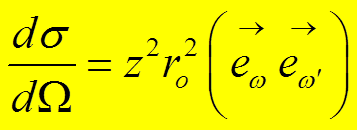Другой предельный случай – 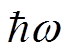  много меньшеэнергии атомных переходов из основного состояния.

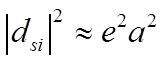Оценка   (  и 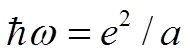  )  дает

.

 

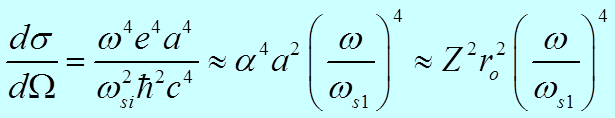Точное выражение для атома водорода может быть получено суммированием вкладов всех состояний

,

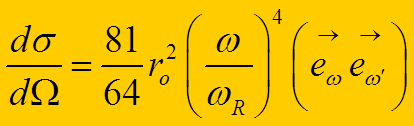где  .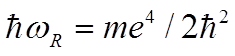

голубой цвет неба и красный цвет заката