







Лекция № 15
Радиационные процессы.
Лучеиспускательная способность и коэффициент поглощения тормозного излучения
Как уже отмечалось, основным механизмом испускания, поглощения и рассеяния света в газах являются электронные переходы, среди которых свободно-свободные и связанно-свободные приводят к образованию непрерывного спектра излучения и поглощения света, а связанно-связанные к образованию линейчатого спектра.
Вычисление вероятностей электронных переходов и сечений радиационных процессов для сложных атомных систем представляет собой трудную квантовомеханическую задачу, решение которой должно быть получено для каждого состояния конкретного атома. В настоящее время известно очень небольшое число подобных решений. Поэтому здесь наибольшее распространение получило использование квазиклассических подходов, которые кроме достаточной простоты, обладают большой наглядностью и имеют ясный физический смысл, что особенно важно для первоначального изучения явлений. Квазиклассические расчеты в основном применимы для водородоподобных систем. Приближение к реальным системам проводится за счет поправочных выражений и коэффициентов, получаемых из квантовомеханических расчетов и сравнений с экспериментом.
 Рассмотрим вначале
свободно-свободные переходы, когда электрон в начальном и конечном состоянии
является свободным.
Рассмотрим вначале
свободно-свободные переходы, когда электрон в начальном и конечном состоянии
является свободным.
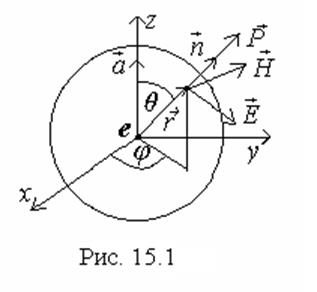
Из теории поля известно, что движущийся заряд (рис. 1.1) создает электромагнитное поле, которое характеризуется напряженностью электрического поля
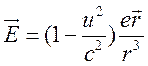 (15.1)
(15.1)
и напряженностью магнитного поля ![]() , которое согласно преобразованию Лоренца
есть:
, которое согласно преобразованию Лоренца
есть:
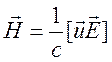 , (15.2),
, (15.2),
где u – скорость заряда, ![]() =
= ![]() и
и ![]() . Для
нерелятивистских скоростей (u << c)
электрическое поле движущегося заряда (15.1) совпадает с Кулоновским
. Для
нерелятивистских скоростей (u << c)
электрическое поле движущегося заряда (15.1) совпадает с Кулоновским
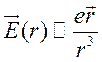 (15.3).
(15.3).
В этом случае из (15.2) с учетом (15.3) следует выражение для магнитного поля
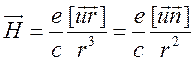 ,
,
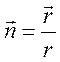 единичный вектор в направлении
единичный вектор в направлении ![]() (15.4),
(15.4),
причем скорость берется на момент
времени ![]() и
и 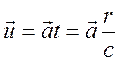 , где а
– ускорение. Тогда
, где а
– ускорение. Тогда
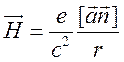 (15.5)
(15.5)
Поток электромагнитной энергии в точке r определяется вектором Пойнтинга
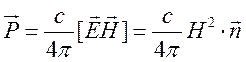 (15.6).
(15.6).
Подставляя (15.5) в (15.6) и
раскрывая векторное произведение [![]()
![]() ]
будем иметь:
]
будем иметь:
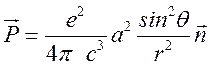 (15.7).
(15.7).
Полный поток находится из (15.7) путем интегрирования по сфере радиуса r
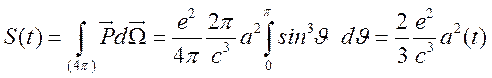 (15.8)
(15.8)
Согласно1-го закона Ньютона свободный электрон, должен либо покоится, либо двигаться с постоянной скоростью, таким образом, чтобы он излучал или поглощал энергию, необходимо наличие некоего «рассеивающего» центра, в поле которого и будет происходить изменение энергии электрона и связанное с этим излучение или поглощение энергии. Изменение энергии при пролете электрона около рассеивающего центра есть:
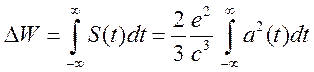 (15.9)
(15.9)
Спектральный состав
излучения можно найти, разлогая вектор ускорения ![]() в
интеграл Фурье:
в
интеграл Фурье:
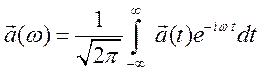 (15.10).
(15.10).
Если воспользоваться соотношением
Парсеваля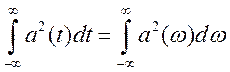 из (15.9) получим
из (15.9) получим
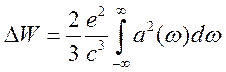 или
переходя к линейным частотам
или
переходя к линейным частотам ![]()
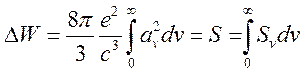 откуда
спектральный поток излучения есть:
откуда
спектральный поток излучения есть:
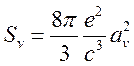 (15.11),
(15.11),
где ![]() определяется
через
определяется
через ![]() по формуле (15.10).
по формуле (15.10).
Таким образом, задача
сводится к определению ускорения ![]() при пролете электрона
вблизи рассеивающего центра. Эта задача даже в классической постановке в общем
случае аналитического решения не имеет. Найдем приближенное решение задачи в
т.н. «ударном приближении». Будем считать, что рассеяние происходит
«мгновенно», это будет справедливо, если время взаимодействия электрона с
рассеивающим центром мало в сравнении с периодом электромагнитных колебаний.
Математически это приближение можно представить
при пролете электрона
вблизи рассеивающего центра. Эта задача даже в классической постановке в общем
случае аналитического решения не имеет. Найдем приближенное решение задачи в
т.н. «ударном приближении». Будем считать, что рассеяние происходит
«мгновенно», это будет справедливо, если время взаимодействия электрона с
рассеивающим центром мало в сравнении с периодом электромагнитных колебаний.
Математически это приближение можно представить
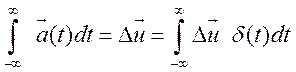 (15.12)
(15.12)
откуда
![]() (15.13).
(15.13).
Подставляя (15.13) в (15.10) получим
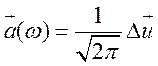 и
из (15.11) спектральный поток есть
и
из (15.11) спектральный поток есть
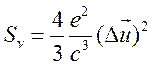 (15.14).
(15.14).
Мы получили непрерывный спектр излучения, независящий от частоты, что является следствием предположения об импульсном взаимодействии. Примем далее, что рассеяние электрона при радиационном торможении практически упругое, т.е. малая часть кинетической энергии электрона переходит в излучение, что, как показывает опыт и точные расчеты, выполняются обычно достаточно хорошо. В этом случае, как следует из рис.15.2
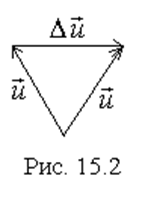
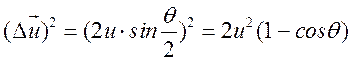 (15.15)
(15.15)
и после подстановки (15.15) в (15.14) получаем
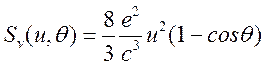 (15.16).
(15.16).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.