Радиационные процессы. Лучеиспускательная способность и коэффициент поглощения тормозного излучения, страница 2

Полученное выражение представляет собой поток  энергии излучения при слабонеупругом торможении электрона на одном рассеивающем центре (атом, молекула, ион), который считается неподвижным (масса электрона на 3 порядка меньше массы центра). Пусть теперь на центр падает поток электронов , где  ( максвелловское распределение электронов по скоростям). Тогда в единицу времени на рассеивающем центре будет излучаться энергия

,                                                                  (15.17),

где  - газокинетическое сечение. Подставим (15.16) в (15.17)

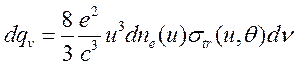,                                                                      (15.18)

где  - транспортное сечение. Выражение (15.18) нужно усреднить по всем углам

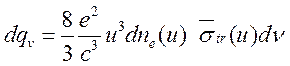                                                                        (15.19)

.

В случае изотропного рассеяния, когда  от  не зависит и  = 0 то , что в дальнейшем и будем подразумевать.

Теперь, чтобы получить энергию, излучаемую единицей объема вещества, нужно (15.19) умножить на объемную плотность рассеивающих центров. Так для энергии, излучаемой в единице объема, при торможении на атомах и ионах электронов данной скорости будем иметь

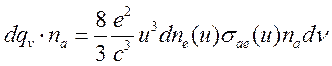                                                                  (15.20)

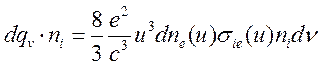                                                                    (15.21)

Если обратимся к излучению в газах, то заметный вклад радиационного переноса тепла в общем энергетическом балансе имеет место при уровнях температур ~ 10⁴ К, когда газ уже достаточно ионизирован и , но при этом сечения столкновения  почти на два порядка выше  и как следует из (15.20) и (15.21) излучением, связанным с рассеянием электронов на атомах практически всегда можно пренебречь по сравнению с тормозным излучением в полях ионов.

Рассмотрим тормозные процессы электронов в полях ионов. В ударном приближении задача сводится к нахождению эффективного сечения столкновений. Чтобы получить простейшую оценку для сечения рассеяния с кулоновским потенциалом, приравняем кинетическую энергию налетающего электрона и потенциальную энергию взаимодействия:

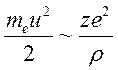,    прицельный параметр                                                (15.22),

откуда 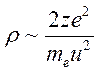 и приближенное выражение для  есть

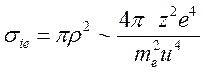                                                                                    (15.23).

Для   и , = 7.8 10^-15см². Выражение (15.23) дает правильную зависимость  от  и фактически учитывает только те электроны, которые, пролетая мимо центра, отклоняются на большие углы, игнорируя дальние пролеты с рассеиванием в малых углах, что приводит к занижению численного значения сечения почти до порядка величины. С сечением (15.23) из (15.21) излучаемая энергия находится:

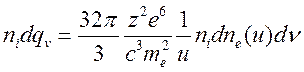                                                                      (15.24)

Аналитическое решение (асимптотическое), полученное в точной постановке для малых и больших частот [2] есть:

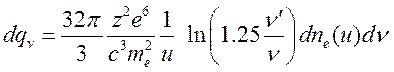      для 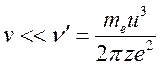          (15.25.1)

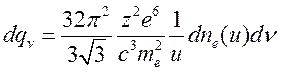                      для 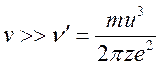          (15.25.2)

Видно, что для больших частот, когда ударное приближение удовлетворительно, точный результат (15.25.2) отличается от полученного нами приближенного численным множителем..

При малых частотах из (15.25.1) видно, что роль логарифма становится заметным лишь при очень низких частотах  (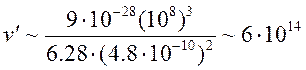с^-1 )

и это лежит ниже частот, при которых вклад излучения в теплопроводность становится заметным. При этом следует отметить еще один физически очевидный факт, что электрон со скоростью  не в состоянии излучить квант энергии, ниже некоторой частоты, определяемой из условия 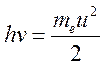, что также обрезает уровень допустимых частот снизу. Как показали многочисленные исследования, для практических расчетов тормозного излучения в задачах радиационной газовой динамики до температур К можно пользоваться формулой (15.25.2) для определения  и

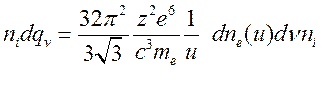                                                                     (15.26),

где 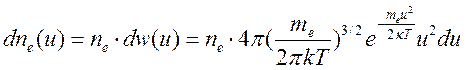. Интегрируя (15.26) по всем скоростям  где 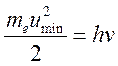 мы получим излучательную способность плазмы:

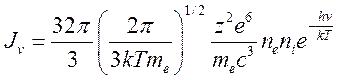                                                                  (15.27).

Интегральная лучеиспускательная способность для тормозного излучения равна

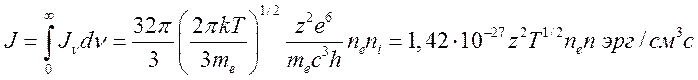                    (15.28)

Для нахождения коэффициента поглощения воспользуемся законом Кирхгофа:

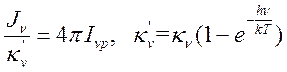                                                                         (15.29),

откуда спектральный коэффициент истинного поглощения тормозного излучения определяется как:

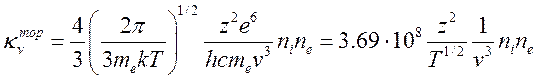 (см ^{– 1})                         (15.30).

Формула (15.30), может быть представлена через т.н. сечение поглощения

                                                                                            (15.31),

 где 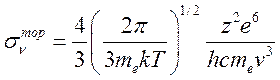 . Это сечение поглощения впервые было получено Крамерсом в 1923 г. и известно как формула Крамерса.

          Из (15.29) и (15.30) имеем

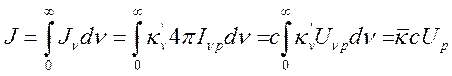                                                           (15.31).

Откуда, средний коэффициент поглощения для тормозного излучения есть

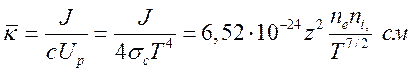                                                                  (15.32).

 -- соответствует среднему Планковскому коэффициенту для тормозного излучения.

Соответствующая длина пробега равна

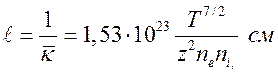                                                                                     (15.33).

Приведу еще выражение средней длины пробега излучения, когда газ полностью ионизован и тормозной механизм поглощения является единственным

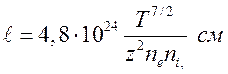                                                                                           (15.34)

и соответствует Росселандову пробегу