Радиационные потери энергии при движении электронов в веществе (Глава 11 учебного пособия)

11. Радиационные потери энергии при движении электронов в веществе

Заряженная частица излучает при столкновении с атомом. Интенсивность, определяемую тормозным излучением, можно определить из формулы

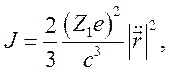                                            (11.1)

где  — ускорение частицы с зарядом Ze. Из (11.1) видно, что в одинаковом поле при  излучение пропорционально , т.е. тяжелые частицы не имеют радиационных потерь.

Второй важный фактор состоит в том, что в отличие от рассмотренных в п. 10 ионизационных потерь, обусловленных рассеянием на электронах, радиационные потери определяются столкновениями с ядром, так как 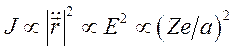. Следовательно, радиационное рассеяние на ядре , тогда как такое же рассеяние на всех электронах .

Радиационные потери аналогично (10.1) определяются выражением

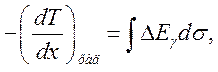                                        (11.2)

где и . Учитывая, что , из (11.1) получим

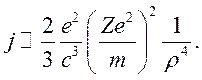                                        (11.3)

Подставив (11.3) в (11.2), окончательно получим

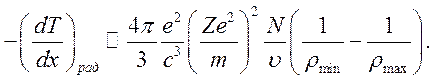                       (11.4)

Принимая во внимание, что  и величина  должна определяться квантовыми эффектами (10.21), окончательно получим

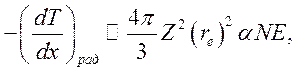                                        (11.5)

где  — классический радиус электрона и . Учитывая, что для суперрелятивистской частицы кинетическая энергия Т равна полной , из (11.5) получим

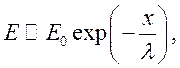                                          (11.6)

где 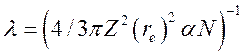 — радиационная длина. В частности, величина  равна в воздухе ~ 300 м, а в свинце ~ 0.5 см.

Приблизительно можно сравнить ионизационные и радиационные потери из следующего соотношения

11.1. Излучение Вавилова – Черенкова

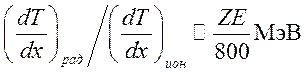
Рассмотрим заряженную частицу, двигающуюся равномерно и прямолинейно, которая теряет свою анергию на излучение. Тогда должно выполняться равенство

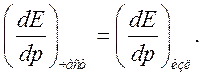                                         (11.7)

Хорошо известно, что для вакуума выполнить это равенство невозможно. Действительно, при  имеем . В то же время для излучения  и . Таким образом, законы сохранения энергии и импульса запрещают заряженной частице, двигающейся равномерно и прямолинейно, отдавать свою энергию в виде излучения фотонов. Однако этот запрет снимается при движении частицы в среде с показателем преломления п > 1. В этом случае скорость фотонов  и скорость частицы  может не только достигать скорости света с' в среде, но и превосходить ее. В случае  > с' условие (11.7) выполняется для такого направления ,вдоль которого , где . Следовательно, излучение должно распространяться под углом

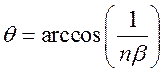                                            (11.8)

где .

Физически механизм свечения Вавилова — Черенкова заключается в когерентном излучении диполей, возникающих в результате поляризации атомов среды двигающейся в ней заряженной частицей.

Возвращение диполей в нормальное состояние после ухода частицы из данной области сопровождается испусканием электромагнитного импульса. Если частица движется медленно, то возникающая поляризация распределена симметрично относительно местонахождения частицы и результирующее поле всех диполей равно нулю. При движении со скоростью, превышающей скорость распространения электромагнитного поля, должен наблюдаться эффект запаздывания поляризации среды, в результате чего диполи будут иметь преимущественную ориентацию.

Не будем останавливаться на выводе основных соотношений, характеризующих рассматриваемое излучение, а лишь кратко рассмотрим его свойства.

Число фотонов в интервале частот от до , испускаемых частицей с зарядом , двигающейся со скоростью в среде с показателем преломления n, при прохождении единицы пути равно [11]:

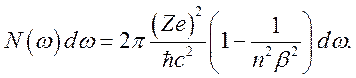                              (11.9)

Из (11.9) видно, что спектр одинаков для частиц с равными значениями Z и  и различной массой, т.е. протонов, электронов, мезонов и т.п. Зависимость от среды определяется только показателем преломления света. Величина  растет от нуля при  до  при  и не зависит от . Энергия излучения , т.е. сконцентрирована в области высоких частот. Этим объясняется сине-фиолетовый цвет излучения. Предельная частота излучения Вавилова — Черенкова определяется изменением показателя преломления среды в коротковолновой области. В частности, рентгеновское излучение отсутствует, так как для него обычно n<1.

Высокая направленность излучения позволяет использовать его для измерения скорости частиц. Если частицу пропустить через тонкий слой вещества, то излучение будет распространяться по образующей конуса, ось которого совпадает с направлением движения частицы, а угол раствора равен  (11.8). Например, для воды  и минимальная скорость, при которой угол излучения , равна . Это соответствует кинетической энергии , что позволяет использовать этот эффект для измерения  уже сравнительно малоэнергичных электронов.