








44. Найти
![]() , если
, если ![]() , где
, где ![]() .
.
45. Найти
dz, если ![]() , где
, где ![]() .
.
46. Найти
![]() , если: а)
, если: а) ![]() , б)
, б)
![]() .
.
47. Найти
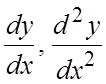 , если: а)
, если: а) ![]() , б)
, б) ![]() .
.
48. Найти
![]() и
и ![]() в точке
(1,-2,2), если
в точке
(1,-2,2), если ![]() .
.
49. Найти
![]() и
и ![]() , если:
а)
, если:
а) ![]() , б)
, б) ![]() .
.
Рекомендация.
Ввести ![]() .
.
9.7. Приложения частных производных и дифференциала
9.7.1. Приложение дифференциала к приближенным вычислениям
Для дифференцируемой функции ![]() при
достаточно малом
при
достаточно малом
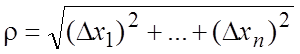 из формул (5.1) – (5.3) следует
из формул (5.1) – (5.3) следует![]() или, что то же самое,
или, что то же самое,
![]() . (7.1)
. (7.1)
Пример 14. Вычислить приближенно 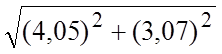 .
.
Ñ Искомое число будем рассматривать как
значение функции 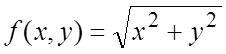 при
при ![]() и
и ![]() , если
, если ![]() . Точка
. Точка
![]() выбрана из соображений близости ее к точке
выбрана из соображений близости ее к точке
![]() и простоты вычисления значений функции f и ее частных производных в
точке М. По формуле (7.1) имеем
и простоты вычисления значений функции f и ее частных производных в
точке М. По формуле (7.1) имеем ![]() .
.
Находим 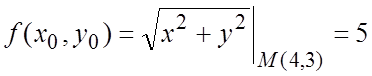 ,
,
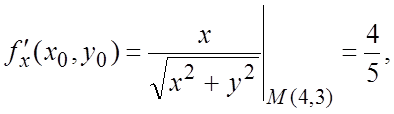
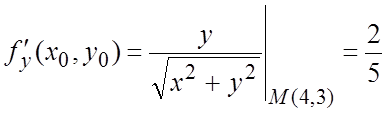 . Следовательно,
. Следовательно, 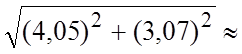 »
»![]()
![]() . #
. #
9.7.2. Касательная поверхность и нормаль к поверхности
1°. Касательной
плоскостью к поверхности в ее точке ![]() (точка
касания) называется плоскость, содержащая в себе все касательные к кривым,
проведенным на поверхности через эту точку. Уравнение касательной плоскости в
точке касания
(точка
касания) называется плоскость, содержащая в себе все касательные к кривым,
проведенным на поверхности через эту точку. Уравнение касательной плоскости в
точке касания ![]() имеет вид:
имеет вид:
а) к поверхности F(x,y,z) = 0:
![]() , (7.2)
, (7.2)
б) к поверхности
![]() :
: ![]() .
.
2°. Нормалью
к поверхности называется прямая, перпендикулярная к касательной плоскости и
проходящая через точку касания. Параметрические уравнения нормали в точке
касания ![]() имеют вид:
имеют вид:
а) к поверхности
![]() :
:
![]() ; (7.3)
; (7.3)
б) к поверхности ![]() :
:
![]()
![]()
![]() .
.
Пример 15. Найти уравнения касательной плоскости и нормали к поверхности
![]() в точке М(2,4,6).
в точке М(2,4,6).
Ñ Обозначив через ![]() левую
часть уравнения поверхности, найдем
левую
часть уравнения поверхности, найдем
![]()
![]()
![]()
![]()
![]()
![]() По формуле (7.2) имеем
уравнение касательной плоскости
По формуле (7.2) имеем
уравнение касательной плоскости ![]() или
или ![]() . По формулам (7.3) находим уравнения
нормали в параметрической форме
. По формулам (7.3) находим уравнения
нормали в параметрической форме ![]() , отсюда можно получить
канонические уравнения нормали
, отсюда можно получить
канонические уравнения нормали 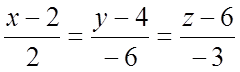 . #
. #
9.7.3. Экстремум функции 2-х переменных
Пусть ![]() - внутренняя точка области определения
функции
- внутренняя точка области определения
функции ![]() . Точка
. Точка ![]() называется
точкой минимума (максимума) функции f,
если существует такая окрестность
называется
точкой минимума (максимума) функции f,
если существует такая окрестность ![]() точки
точки ![]() , что для любой точки
, что для любой точки ![]() выполняется
выполняется ![]()
![]() .
.
Точка ![]() называется точкой экстремума
функции f, если она является точкой минимума или
точкой максимума этой функции.
называется точкой экстремума
функции f, если она является точкой минимума или
точкой максимума этой функции.
Теорема 9.7. (Необходимое условие экстремума.) Если ![]() - точка экстремума функции, то каждая
частная производная
- точка экстремума функции, то каждая
частная производная ![]() и
и ![]() либо
равна нулю, либо не существует.
либо
равна нулю, либо не существует.
Точка ![]() называется критической точкой
функции f, если в ней выполняются необходимые
условия экстремума функции f.
называется критической точкой
функции f, если в ней выполняются необходимые
условия экстремума функции f.
Теорема 9.8. (Достаточные условия экстремума.) Пусть: а) ![]() - критическая точка функции f, б) существуют и непрерывны производные
- критическая точка функции f, б) существуют и непрерывны производные ![]() в точках
в точках ![]() и
и ![]() , в)
, в) 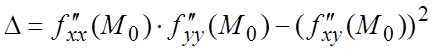 .Тогда:
1) если
.Тогда:
1) если ![]() и
и ![]()
![]() , то
, то ![]() - точка
минимума функции f ; 2)
если
- точка
минимума функции f ; 2)
если ![]() и
и ![]()
![]() , то
, то ![]() - точка
максимума функции f ; 3)
если
- точка
максимума функции f ; 3)
если ![]() , то
, то ![]() не является
точкой экстремума; 4) если
не является
точкой экстремума; 4) если ![]() , то требуется
дополнительное исследование.
, то требуется
дополнительное исследование.
Отметим, что в случае ![]() существуют такие две
прямые, проходящие через точку
существуют такие две
прямые, проходящие через точку ![]() , что при движении точки
M по первой из этих прямых значения функции
, что при движении точки
M по первой из этих прямых значения функции ![]() сначала уменьшаются, затем возрастают. При
движении точки М по другой прямой значения функции сначала возрастают, в
точке
сначала уменьшаются, затем возрастают. При
движении точки М по другой прямой значения функции сначала возрастают, в
точке ![]() достигают максимума, затем уменьшаются. В
этом случае точку
достигают максимума, затем уменьшаются. В
этом случае точку ![]() называют седловой.
называют седловой.
Пример 16. Исследовать на экстремум функцию ![]() .
.
Ñ Из необходимого условия экстремума функции
(теорема 9.7) имеем систему 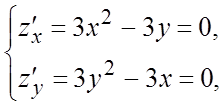 решая которую
получаем критические точки
решая которую
получаем критические точки ![]()
![]() . Определим характер критических точек по
достаточным условиям экстремума. Находим
. Определим характер критических точек по
достаточным условиям экстремума. Находим ![]()
![]() . В точке
. В точке ![]() :
: ![]() ,
, ![]() ,
, ![]() ,
, 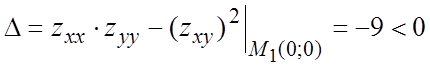 .
Следовательно,
.
Следовательно, ![]() - седловая точка. В точке
- седловая точка. В точке ![]() :
: ![]()
![]() ,
, ![]() ,
, ![]() , поэтому
, поэтому ![]() - точка
минимума функции z;
- точка
минимума функции z; ![]() . #
. #
9.7.4. Наибольшее и наименьшее значения функции 2-х
переменных в замкнутой области
В 9.3
была сформулирована теорема Вейерштрасса (теорема 9.1), согласно которой всякая
функция ![]() , непрерывная в замкнутой области U, ограниченной ломаной Г=
, непрерывная в замкнутой области U, ограниченной ломаной Г=![]() ,
достигает в этой области своих наибольшего – наименьшего значений, для
отыскания которых пользуемся следующим алгоритмом.
,
достигает в этой области своих наибольшего – наименьшего значений, для
отыскания которых пользуемся следующим алгоритмом.
1. Находим критические точки, принадлежащие U.
2. На каждом
звене ![]() ломаной Г сводим функцию f к функции
ломаной Г сводим функцию f к функции ![]() одной переменной и
выделяем на
одной переменной и
выделяем на ![]() критические точки функции
критические точки функции ![]() .
.
3. Список точек, полученный в пунктах 1 и 2 дополняем вершинами ломаной Г.
4. Вычисляем значения функции в точках полученного списка и выбираем среди них наибольшее и наименьшее, которые и будут искомыми.
Пример 17. Найти наибольшее и наименьшее значения функции ![]() в области D,
заданной неравенствами
в области D,
заданной неравенствами ![]() .
.
Ñ Область D
ограничена частью параболы ![]() и отрезком прямой x = 4 (рис.9.3). 1) Находим критические точки из
необходимого условия экстремума функции:
и отрезком прямой x = 4 (рис.9.3). 1) Находим критические точки из
необходимого условия экстремума функции: 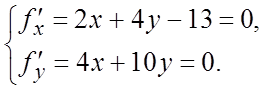 Решение
системы: x =32,5, y = –13. Найденная критическая
точка
Решение
системы: x =32,5, y = –13. Найденная критическая
точка ![]() не принадлежит D.
не принадлежит D.
2) Исследуем
функцию на границе. а) На участке ![]() . Функция
. Функция ![]() сводится к функции одной переменной
сводится к функции одной переменной ![]()
![]() .Находим критические
точки функции
.Находим критические
точки функции ![]() :
:![]()
![]() . На
. На ![]() x = 4 и точки
x = 4 и точки ![]() . б) На линии
. б) На линии ![]()
![]() . Функция
. Функция ![]() сводится к функции
сводится к функции ![]() ,
,
![]() . Находим критические точки функции
. Находим критические точки функции ![]() :
: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . На
. На ![]()
![]() и получаем точки
и получаем точки ![]() ,
, ![]() .
.
3) Вершины
ломаной в точках ![]() и
и ![]() . 4)
Вычисляем значения функции f в точках
. 4)
Вычисляем значения функции f в точках ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() . Итак,
. Итак, ![]() ,
, ![]() .#
.#
9.7.5. Формула Тейлора для функции 2-х переменных.
Если
функция ![]() дифференцируема n+1
раз в некоторой окрестности
дифференцируема n+1
раз в некоторой окрестности ![]() точки
точки ![]() , то для всякой точки
, то для всякой точки ![]() справедлива формула Тейлора
справедлива формула Тейлора
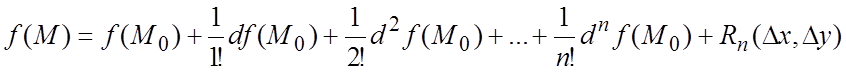
или, записав несколько членов в развернутом виде,
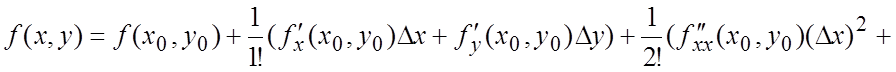
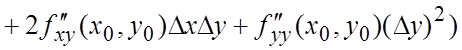 +
+ 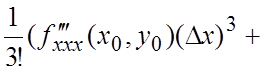 (7.4)
(7.4)
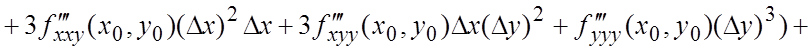 …+
…+
![]() . Здесь
. Здесь ![]() - остаточный
член в формуле Тейлора порядка n. При этом
- остаточный
член в формуле Тейлора порядка n. При этом ![]() ,где
,где ![]() -
бесконечно малая функция при
-
бесконечно малая функция при ![]() и
и ![]() , вид которой зависит от функции f и точки
, вид которой зависит от функции f и точки ![]() . В форме Пеано
. В форме Пеано ![]() , где
, где 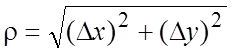 . При
. При ![]() формула (7.4) называется формулой Маклорена.
формула (7.4) называется формулой Маклорена.
Пример 18. Функцию ![]() разложить по формуле
Тейлора в окрестности точки(2,-1).
разложить по формуле
Тейлора в окрестности точки(2,-1).
Ñ Имеем ![]() .
Вычислим последовательно частные производные данной функции:
.
Вычислим последовательно частные производные данной функции: 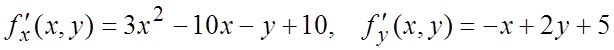 ,
,
![]() . Все последующие производные тождественно
равны нулю. Значения производных в точке(2,-1):
. Все последующие производные тождественно
равны нулю. Значения производных в точке(2,-1):
![]()
![]() .
По формуле (7.4) получаем искомое разложение
.
По формуле (7.4) получаем искомое разложение
![]() .#
.#
Пример 19. Функцию ![]() разложить по формуле
Тейлора в окрестности точки (1;1) до членов второго порядка включительно.
разложить по формуле
Тейлора в окрестности точки (1;1) до членов второго порядка включительно.
Ñ Имеем ![]() . В
соответствии с формулой (7.4) вычислим производные 1-го и 2-го порядков данной
функции и их значения в точке (1,1).
. В
соответствии с формулой (7.4) вычислим производные 1-го и 2-го порядков данной
функции и их значения в точке (1,1).
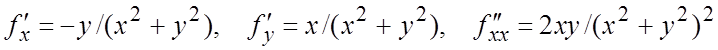 ,
,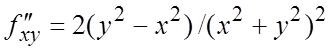 ,
, 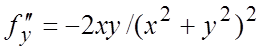 ;
; ![]() ,
,
![]() ,
, ![]()
![]()
![]() . По
формуле (7.4) имеем
. По
формуле (7.4) имеем ![]() , где
, где 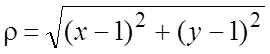 . #
. #
Задачи для самостоятельного решения
Вычислить приближенно:
50. ![]() . 51.
. 51. 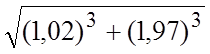 . 52.
. 52.
![]() . 53.
. 53. ![]() .
.
54.
Цилиндрический стакан имеет внутренние размеры: радиус основания
R =2,5м, высоту H
= 4м и толщину стенок l=1 дм . Найти приближенно
объем
материала, затраченного на изготовление стакана.
55. В усеченном конусе радиусы оснований R =20 см, r =10см, высота h =30 см. Как приближенно изменится объем конуса, если R увеличить на 2 мм, r – на 3 мм и h уменьшить на 1мм.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.