Выборка №24, а=-2, s2 =1.1, e =0.04
|
-1.812 |
-0.007 |
-2.091 |
-3.040 |
-0.100 |
-4.143 |
-1.516 |
-2.636 |
-0.661 |
-1.469 |
|
-1.851 |
-0.871 |
0.592 |
-2.884 |
-1.279 |
-3.195 |
-2.697 |
-3.392 |
-2.072 |
-1.877 |
|
-3.718 |
-1.178 |
-1.504 |
-3.307 |
-1.562 |
-2.144 |
-0.938 |
-1.549 |
-2.586 |
-1.295 |
|
-2.644 |
-2.518 |
-2.249 |
-1.356 |
-0.265 |
-2.580 |
-1.915 |
-2.782 |
-1.975 |
-2.190 |
|
-1.582 |
-2.393 |
-3.232 |
-2.710 |
0.112 |
-4.730 |
-2.675 |
-1.869 |
-1.830 |
-1.620 |
ЗАДАНИЕ №1
Построить доверительный интервал уровня доверия 1-e по исходной выборке объема 50 для параметра нормального распределения:
а) ![]() , если
, если ![]() известно,
известно,
б) ![]() , если
, если ![]() неизвестно,
неизвестно,
в) ![]() , если
, если ![]() известно,
известно,
г) ![]() , если
, если ![]() неизвестно.
неизвестно.
Пусть ![]() такие статистики, что
такие статистики, что ![]() . Тогда
. Тогда
интервал ![]() называется доверительным
интервалом (ДИ) для
называется доверительным
интервалом (ДИ) для ![]() уровня
уровня ![]() .
.
а) Если ![]() , то
, то 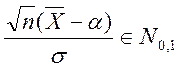 ,
,
Для оценки ![]() при известной дисперсии
воспользуемся статистикой
при известной дисперсии
воспользуемся статистикой 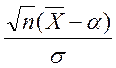 .
.
Она распределена по стандартному нормальному закону.
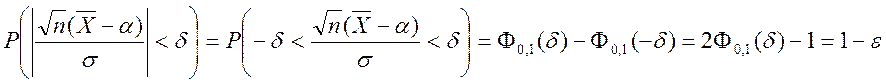
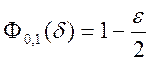 . По
таблице находим
. По
таблице находим ![]() .
.
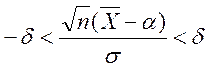
ДИ 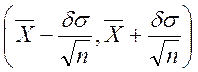 .
.
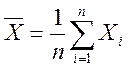 = -1.9959
= -1.9959
![]()
![]() = 2,053749
= 2,053749 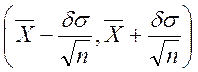 = (-2.300520; -1.69127979)
= (-2.300520; -1.69127979)
б) Если ![]() , то
, то 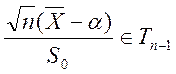 .
.
Для оценки ![]() при неизвестной
дисперсии воспользуемся статистикой
при неизвестной
дисперсии воспользуемся статистикой 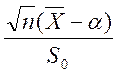 .
.
Она имеет распределение Стьюдента с ![]() степенями
свободы.
степенями
свободы.
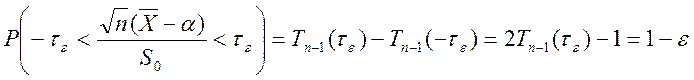
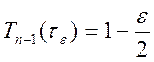 . По таблице находим
. По таблице находим ![]() .
.
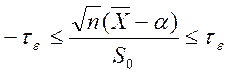
ДИ 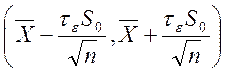 .
.
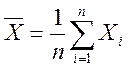 = -1.9959
= -1.9959
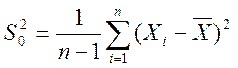 = 1.168098
= 1.168098
![]()
![]() = 2.404892
= 2.404892 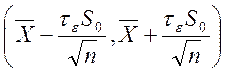 = (-2.363478;-1.628321 )
= (-2.363478;-1.628321 )
в) Если ![]() , то
, то 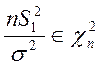 , где
, где 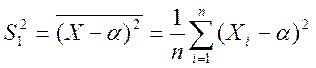 .
.
Для оценки ![]() при известном среднем воспользуемся
статистикой
при известном среднем воспользуемся
статистикой 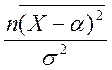 .Она имеет распределение
хи-квадрат с
.Она имеет распределение
хи-квадрат с ![]() степенями свободы.
степенями свободы.
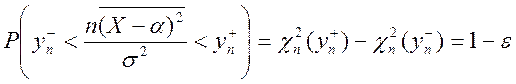
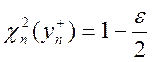 и
и  .
По таблице находим
.
По таблице находим ![]() и
и ![]() .
.
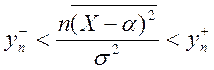
ДИ 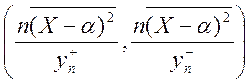 .
.
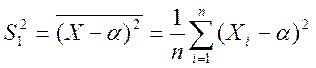 =1,144753
=1,144753
![]()
![]() = 72.61325
= 72.61325
![]()
![]() = 31.66386
= 31.66386 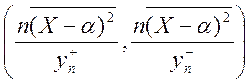 = (0.788253;1.807663
)
= (0.788253;1.807663
)
г) Если ![]() , то
, то 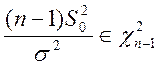
Для оценки ![]() при неизвестном
при неизвестном ![]() воспользуемся статистикой
воспользуемся статистикой 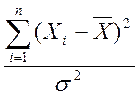 .Она имеет распределение хи-квадрат с
.Она имеет распределение хи-квадрат с ![]() степенями свободы.
степенями свободы.
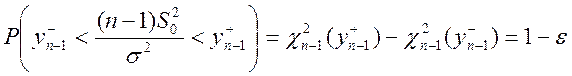
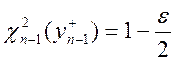 и
и 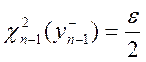 .
По таблице находим
.
По таблице находим ![]() и
и ![]() .
.
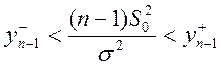
ДИ 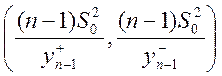 .
.
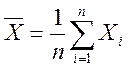 = -1.9959
= -1.9959
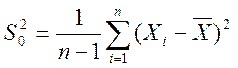 = 1.168098
= 1.168098
![]()
![]() =
71.40608
=
71.40608
![]()
![]() =
30.87076
=
30.87076 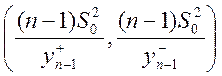 = (0.801567;1.8540781);
= (0.801567;1.8540781);
ЗАДАНИЕ №3.
По данным двум выборкам объёма 20 и 30 проверить, с помощью критериев
размера ![]() , гипотезу:
, гипотезу:
а) о совпадении дисперсий (критерий Фишера),
б) о совпадении средних, если известно, что неизвестные дисперсии совпадают (критерий Стьюдента).
a) Критерий Фишера.
Проверяется гипотеза ![]() .
.
Введем функцию отклонения 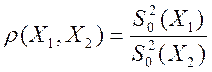 .
.
Теорема: Если гипотеза ![]() верна,
то случайная величина
верна,
то случайная величина ![]() имеет распределение Фишера
имеет распределение Фишера ![]() с n-1, m-1 степенями свободы.
с n-1, m-1 степенями свободы.
Критерий Фишера:
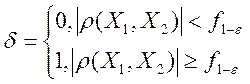 , где
, где ![]() – квантиль
распределения Фишера.
– квантиль
распределения Фишера.
![]() = 1.5133
= 1.5133
![]() = 0.957927
= 0.957927
![]() = 1.579765
= 1.579765
![]() = 2.045852
= 2.045852
1.579765< 2.045852, основная гипотеза принимается, то есть дисперсии совпадают.
б) Критерий Стьюдента.
Проверяется гипотеза ![]() .
.
Теорема: Случайная величина 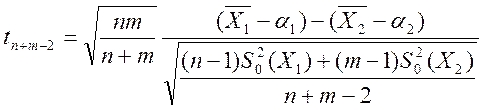 имеет распределение Стьюдента
имеет распределение Стьюдента ![]() с n+m-2 степенями свободы.
с n+m-2 степенями свободы.
Введем функцию 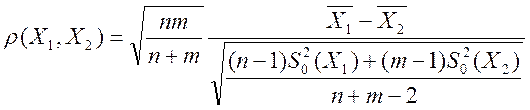 . Из теоремы следует
свойство: если
. Из теоремы следует
свойство: если ![]() верна, то величина
верна, то величина![]() имеет распределение Стьюдента с n+m-2 степенями свободы.
имеет распределение Стьюдента с n+m-2 степенями свободы.
Критерий Стьюдента:
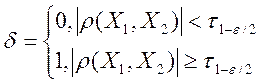 , где
, где ![]() – квантиль
распределения Стьюдента.
– квантиль
распределения Стьюдента.
![]() = -1,85055
= -1,85055
![]() = -2,0928
= -2,0928
![]() = 1.5133
= 1.5133
![]() = 0.957927
= 0.957927
![]() = 0,773260
= 0,773260
![]() = 2.404892
= 2.404892
0,773260< 2.404892,основная гипотеза принимается, то есть средние совпадают.
|
0,446 |
0,868 |
0,034 |
0,568 |
0,078 |
0,691 |
0,591 |
0,210 |
0,870 |
0,025 |
|
0,551 |
0,436 |
0,074 |
0,093 |
0,530 |
0,603 |
0,589 |
0,709 |
0,005 |
0,837 |
|
0,530 |
0,603 |
0,101 |
0,926 |
0,359 |
0,477 |
0,081 |
0,681 |
0,411 |
0,102 |
ЗАДАНИЕ №2.
По данной выборке объёма 30 проверить основную гипотезу о равномерности распределения с помощью:
а) критерия Колмогорова,
б) критерия хи-квадрат.
Введём функционал ![]() , который измеряет
расстояние между эмпирическим и теоретическим распределениями, такой что:
, который измеряет
расстояние между эмпирическим и теоретическим распределениями, такой что:
1.По заданному ![]() можно найти
можно найти ![]() такое, что
такое, что ![]() .
.
2.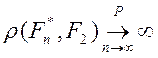 , где
, где ![]() распределение
отличное от
распределение
отличное от ![]() .
.
Критерий согласия, основанный на таком функционале, строится следующим образом:
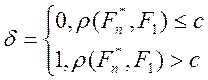 .
.
Пусть по данной реализации выборки получено число ![]() .
.
Число ![]() называют реально
достигнутым уровнем значимости.
называют реально
достигнутым уровнем значимости.
И 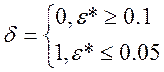
Критерий Колмогорова.
Выбирается функционал 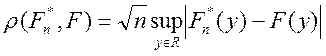 .
.
Теорема Колмогорова: Если ![]() -
истинное распределение выборки
-
истинное распределение выборки ![]() , то
, то 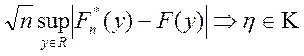 .
.
Критерий Колмогорова:
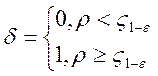 , где
, где ![]() – квантиль
уровня
– квантиль
уровня ![]() распределения
распределения ![]() .
.
|
0,005 |
0,005 |
0,028333 |
|
0,025 |
0,008333 |
0,041667 |
|
0,034 |
0,032667 |
0,066 |
|
0,074 |
0,026 |
0,059333 |
|
0,078 |
0,055333 |
0,088667 |
|
0,081 |
0,085667 |
0,119 |
|
0,093 |
0,107 |
0,140333 |
|
0,101 |
0,132333 |
0,165667 |
|
0,102 |
0,164667 |
0,198 |
|
0,21 |
0,09 |
0,123333 |
|
0,359 |
0,025667 |
0,007667 |
|
0,411 |
0,044333 |
0,011 |
|
0,436 |
0,036 |
0,002667 |
|
0,446 |
0,012667 |
0,020667 |
|
0,477 |
0,010333 |
0,023 |
|
0,53 |
0,03 |
0,003333 |
|
0,53 |
0,003333 |
0,036667 |
|
0,551 |
0,015667 |
0,049 |
|
0,568 |
0,032 |
0,065333 |
|
0,589 |
0,044333 |
0,077667 |
|
0,591 |
0,075667 |
0,109 |
|
0,603 |
0,097 |
0,130333 |
|
0,603 |
0,130333 |
0,163667 |
|
0,681 |
0,085667 |
0,119 |
|
0,691 |
0,109 |
0,142333 |
|
0,709 |
0,124333 |
0,157667 |
|
0,837 |
0,029667 |
0,063 |
|
0,868 |
0,032 |
0,065333 |
|
0,87 |
0,063333 |
0,096667 |
|
0,926 |
0,040667 |
0,074 |
|
1 |
0 |
0 |
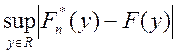 =0.198
=0.198
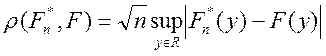 =1.084490
=1.084490
![]()
![]() =0.740566
=0.740566
![]() =0.518868.
=0.518868.
0.518868>0.1, основная гипотеза принимается, то есть распределение равномерное.
Критерий хи-квадрат.
Выбирается функционал 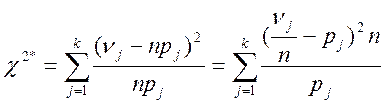 ,где
,где
k – число
непересекающихся интервалов ![]() , покрывающих R,
, покрывающих R,
![]() - вероятность попадания в эти
интервалы для распределения
- вероятность попадания в эти
интервалы для распределения ![]() ,
,
![]() - число элементов выборки,
попавших в интервал
- число элементов выборки,
попавших в интервал ![]() .
.
Теорема Пирсона:Если ![]() , то
, то ![]() .
.
Критерий хи-квадрат:
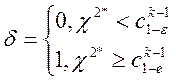 , где c –
квантиль уровня
, где c –
квантиль уровня ![]() распределения
распределения ![]() .
.
|
|
интервалы |
|
|
|
1 |
0-0,2 |
9 |
9 |
|
2 |
0,2-0,4 |
2 |
16 |
|
3 |
0,4-0,6 |
10 |
16 |
|
4 |
0,6-0,8 |
5 |
1 |
|
5 |
0,8-1 |
4 |
4 |
|
|
7.666667 |
||
![]()
![]() =0,104508
=0,104508
0,104508>0.1, основная гипотеза принимается, то есть распределение равномерное.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.