Плазма как система независимых частиц. Траектории частиц в плазме, дрейфовое приближение, страница 4

Дрейф в неоднородном магнитном поле

Проще всего выражение для скорости дрейфа в неоднородном магнитном поля находится, если ввести фиктивную магнитную силу

,                                                                                           (2.32)

где магнитный момент  определяется выражением (2.13). Подставляя формулу (2.32) в общее выражение дрейфовой скорости (2.27), с учетом (2.13) получим

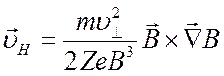          .                                                                              (2.32)

          Дрейфовое движение в магнитном поле может иметь место и в однородном магнитном поле, если силовые магнитные линии искривлены. В этом случае центр циклотронного кружка движется по искривленной силовой линии и можно считать, что на него действует центробежная сила, направленная по радиусу  кривизны , нормальному к силовой линии

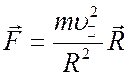                                                                                                       (2.33)

и после подстановки в формулу (2.27) получится векторная формула для скорости центробежного дрейфа

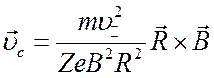          .                                                                                (2.34)

          Скорости градиентного и центробежного дрейфов зависят от заряда частицы, так что противоположно  заряженные частицы дрейфуют в противоположных направлениях и имеет место разделение зарядов в плазме.

          Плотность дрейфового тока выражается как

          ,                                                                                             (2.35)

где  - число частиц в единице объема,  - скорость соответствующего дрейфового движения. Откуда для градиентного дрейфа

                                                                                   (2.36)

и для центробежного дрейфа

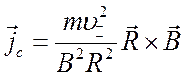          .                                                                                   (2.37)

Поляризационный дрейф

          Если частицы испытывают постоянное или медленно меняющееся ускорение , то уравнение движения можно записать

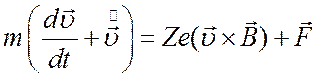          ,                                                                 (2.38)

что совпадает с уравнением (2.1), если к силе  добавить инерционную силу

          .                                                                                             (2.39)

          Важнейшим случаем инерционного дрейфа является поляризационный дрейф, где ускорение происходит от изменения скорости электрического дрейфа, вызванного переменным электрическим полем. Если скорость изменения электрического поля есть , то электрический дрейф происходит с ускорением (см. (2.30))

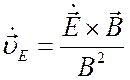          ,                                                                                         (2.40)

создающим инерционную силу

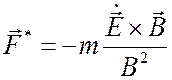          .                                                                                      (2.41)

Эта сила, согласно формуле (2.27) вызывает дрейф частиц со скоростью

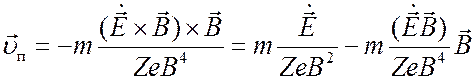          .                                (2.42)

          Рассмотрим простейший случай, когда переменное электрическое поле направлено поперек магнитного. В этом случае второй член обращается в нуль и скорость поляризационного дрейфа оказывается направленной вдоль электрического поля

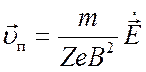          .                                                                                         (2.43)

Таким образом, поперечное переменное электрическое поле вызывает в замагниченной плазме дрейфовый ток плотностью

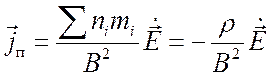          ,                                                                       (2.44)

где 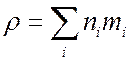- плотность плазмы.

          Плотность дрейфового тока пропорциональна массе частицы, так что он переносится практически целиком ионами. Этот дрейфовый ток во многих случаях оказывается гораздо существеннее, чем соответствующий ток проводимости.