Плазма как система независимых частиц. Траектории частиц в плазме, дрейфовое приближение, страница 3

          Чтобы просто и наглядно представить природу дрейфового движения  и оценить величину дрейфовой скорости, рассмотрим циклотронную окружность (рис.2.1). Сила  направлена поперек магнитного поля. Тогда согласно рисунку в верхней половине окружности сила действует по направлению вращения, в нижней ─ против. В результате частица будет двигаться сверху  вниз быстрее, чем снизу вверх. Разность этих скоростей приведет к смещению циклотронного кружка с постоянной скоростью в направлении, перпендикулярном как к магнитному, так и к действующей силе. Это смещение и называется дрейфом.

          Оценим величину скорости дрейфа. Сила  создает ускорение . За  время  приращение скорости составит . В рассмотренном примере скорость вращения в направлении вниз будет на величину такого порядка больше, а вверх ─ меньше. Разность этих скоростей дает скорость дрейфа, величина которой   или, если подставить значение циклотронной частоты,

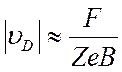          .                                                                                             (2.20)

Количественное рассмотрение дрейфового движения

Направим ось  вдоль магнитного поля. Сила  нормальна к направлению поля. Будем считать магнитное поле и силу постоянными в пространстве и во времени. Распишем уравнение (2.1) в проекциях:

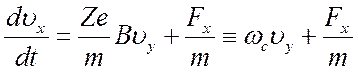          ;                                                           (2.21)

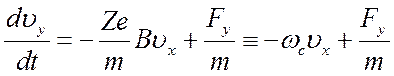          .                                                      (2.22)

Запишем эту систему в комплексном виде

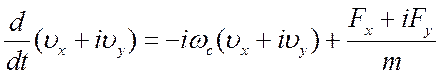          .                                               (2.23)

Решение этого неоднородного уравнения состоит из общего решения однородного уравнения

          ,                                                                    (2.24)

представляющего циклотронное вращение, и частного решения неоднородного уравнения, представляющего дрейфовое движение. Если сила  постоянна во времени и по пространству, то частное решение можно получить, прировняв правую часть к нулю, тогда

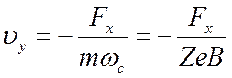          ;                                                                             (2.25)

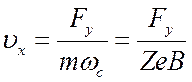          ,                                                                         (2.26)

или в векторной форме

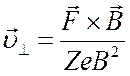          .                                                                                            (2.27)

          В случае если сила  медленно меняется в пространстве и во времени, то полученный выше результат будет приближенным и будет тем ближе к действительности, чем лучше выполняется условие адиабатичности.

          Плотность тока, переносимого дрейфовым движением есть

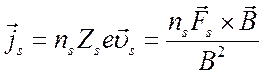          .                                                               (2.28)

Здесь индекс 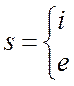 определяет сорт частиц. Полная плотность тока находится суммированием по индексу  для частиц всех сортов (ионов) .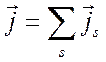

Электрический дрейф

          Простейший случай дрейфового движения тот, когда сила   (нормальная к направлению магнитного поля) является сила электрического поля. Такой дрейф называют электрическим или еще дрейфом в скрещенных полях. Электрическое поле  действует на частицу с зарядовым числом  с силой

          .                                                                                                (2.29)

Отсюда скорость электрического дрейфа согласно формуле (2.27)

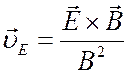          ,                                                                                           (2.30)

или по абсолютному значению

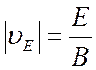          .                                                                                                 (2.31)

Поскольку в формулах (2.30) и (2.31) отсутствует зарядовое число, то электроны и ионы дрейфуют в одном направлении и с одинаковой скоростью. Электрический дрейф не приводит к разделению зарядов, а вызывает только движение плазмы как целого.

Картина резко изменяется если выполнено условие (2.19), т.е. замагничены и дрейфуют только электроны. В этом случае электрический дрейф приводит к разделению зарядов.