Плазма как система независимых частиц. Траектории частиц в плазме, дрейфовое приближение

Лекция 2

Плазма как система независимых частиц.

Траектории частиц в плазме, дрейфовое приближение

Особенно сильно наличие ионизованных частиц в газе проявляется в присутствии внешнего электромагнитного поля.

Если на не слишком плотную плазму действуют достаточно сильные внешние поля, то в разумном приближении можно пренебречь внутренними полями, происходящими от взаимодействия частиц. В этом приближении можно рассматривать плазму как систему независимых заряженных частиц, движущихся по своим траекториям в заданных внешних полях. Единственным полем, которым нельзя пренебречь, является электрическое поле поляризации, возникающее вследствие разделения зарядов и обеспечивающее квазинейтральность плазмы.

Уравнение движения заряженной частицы в заданных внешних полях имеет вид

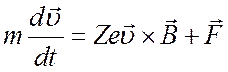          ,                                                                              (2.1)

где m ─ масса частицы; Z ─ ее зарядовое число;  ─ ее скорость; ─ индукция магнитного поля;  ─ равнодействующая всех остальных сил,  действующих на частицу.

В начале рассмотрим простейший случай ─ движение частиц в постоянном однородном магнитном поле. Уравнение движения (2.1) примет вид

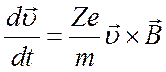  .                                                                                     (2.2)

Отсюда видно, что ускорение лежит в плоскости, перпендикулярной к магнитному полю. Продольная скорость частицы вдоль поля  не зависит от магнитного поля и определяется другими действующими на частицу силами. Определим поперечную скорость  в плоскости перпендикулярной к магнитному полю. Направим ось  вдоль магнитного поля, тогда для составляющих скорости  и  из уравнения  (2.2) получим

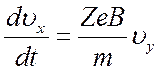          ;                                                                                       (2.3)

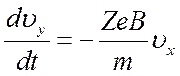          ;                                                                                    (2.4)

Удобно ввести комплексную величину

          .                                                                                          (2.5)

Тогда уравнения (2.3) и (2.3) сведутся к уравнению

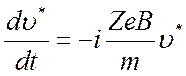          .                                                                                    (2.6)  

Решение уравнения (2.6) есть

                                                                                                (2.7) представляет вращение в плоскости, перпендикулярной к магнитному полю с круговой частотой

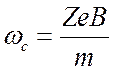          .                                                                                              (2.8)

Эта частота называется циклотронной или ларморовской, иногда также гирочастотой. Для электронов

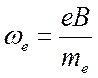          ;                                                                                                (2.9)

для ионов с зарядовым числом  

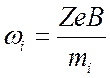          .                                                                                               (2.10)

          Движение заряженной частицы в постоянном однородном магнитном поле может быть представлено как наложение свободного движения вдоль поля и ларморовского вращения поперек поля. Радиус циклотронной орбиты (ларморовского кружка) равен

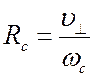          .                                                                                                 (2.11)

          Из закона сохранения  момента количества движения 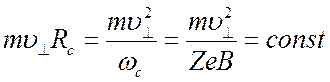 следует, что должна сохранятся величина

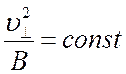,                                                                                            (2.12) или, как говорят быть интегралом движения. Из определения магнитного момента 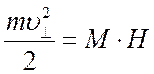 следует также сохранение магнитного момента

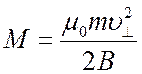 .                                                                                         (2.13)

Здесь Н ─ напряженность магнитного поля,  ─ индукция магнитного поля,  ─ магнитная постоянная (магнитная проницаемость вакуума).

Закон сохранения магнитного момента был получен в предположении постоянства однородного магнитного поля. В более общем случае, когда  магнитное поле достаточно медленно меняется во времени и в пространстве, он справедлив лишь приближенно. Медленное изменение внешних условий называют адиабатическим. Соответственно магнитный момент циклотронной орбиты называют адиабатическим инвариантом (адиабатическими инвариантами называются величины, которые приближенно сохраняются при медленном изменении состояния системы).

Количественно условие адиабатичности сводится к требованию, чтобы относительное изменение магнитного поля было малым: во времени - за период циклотронного вращения; в пространстве ─ на длине, равной циклотронному радиусу:

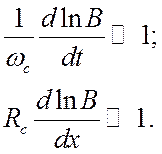                                                                                        (2.14)

Циклотронное вращение проявляется в полной мере только в разреженной плазме, где столкновения между частицами редки. В плотной плазме вследствие высокой частоты столкновений правильное циклотронное вращение нарушается и характеризуется величиной

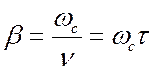,                                                                                        (2.15)

где  ─ средняя частота столкновений с передачей импульса, ─ среднее время между столкновениями. Эта величина представляет собой очень важную характеристику плазмы, называемую параметром Холла.

 Для того чтобы циклотронное вращение могло проявиться, нужно, чтобы период его был мал в сравнении со временем между столкновениями, т.е., чтобы выполнялось условие

.                                                                                                    (2.16)

Плазму, удовлетворяющую этому условию называют замагниченной. В замагниченной плазме тепловое движение поперек поля имеет характер циклотронного вращения. Если условие замагниченности не выполняется, то, не успев закончить полный оборот, частица сбивается с траектории в результате изменения направления движения, вызванного столкновениями.