Оценка качества регулирования. Корневые методы оценки ошибок

Оценка качества регулирования [1, с.203].

          В конечном счёте, качество регулирования определяется величиной ошибки . Однако, коль скоро задающее и возмущающее воздействия случайны, используются различные критерии качества: точность (величина ошибки при типовом режиме), запас устойчивости (удалённость от колебательной границы устойчивости) и быстродействие (грубо говоря – время переходного процесса).

Точность в типовых режимах.

          Неподвижное состояние. Установившаяся статическая ошибка:

.

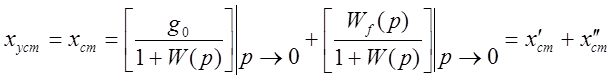Движение с постоянной скоростью: . Установившаяся ошибка:

.

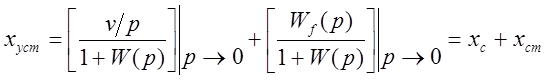Первое слагаемое имеет смысл при астатизме не менее первого порядка:

.

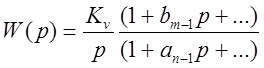При этом скоростная ошибка .

Движение по гармоническому закону. Амплитуда ошибки оценивается по амплитудной характеристике разомкнутой системы:

.

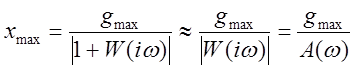Коэффициенты ошибок.

Спустя достаточно много времени, т.е. при малых р:

.

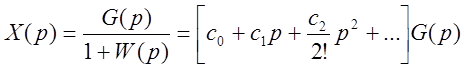Для оригинала:

.

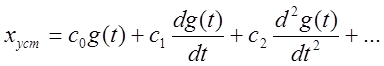Здесь  – коэффициенты ошибок ( – статическая ошибка, ).

Так как передаточная функция по ошибке представляет собой дробно-рациональную функцию, то коэффициенты ошибок вычисляются делением числителя на знаменатель.

Пример [1, c.209].

          Передаточная функция разомкнутой системы:

.

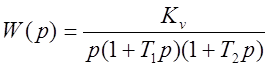Передаточная функция по ошибке:

.

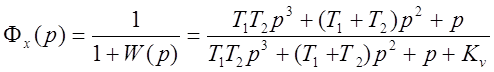Деление числителя на знаменатель:

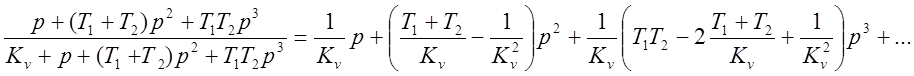Если задающее воздействие имеет вид

,

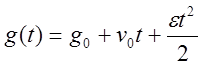то установившаяся ошибка

.

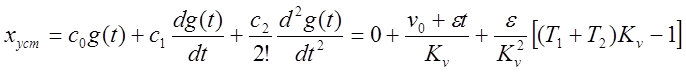Корневые методы оценки ошибок [1, c.215].

          Можно сформулировать требования по запасу устойчивости и быстродействию системы, накладывая определённые условия на корни характеристического уравнения.

Характеристическое уравнение:

.

Среднегеометрический корень:

.

Замена  даёт:

.

Увеличение среднегеометрического корня ведёт к соответствующему увеличению скорости протекания переходных процессов. Заметим, что  – безразмерное время.

Для увеличения , очевидно, следует увеличивать  – свободный член характеристического уравнения. В статических системах , а в астатических , где K – общий коэффициент усиления разомкнутой системы.

Понятие степени быстродействия :

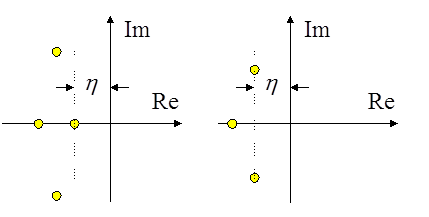
При всех вещественных корнях, или при одной паре мнимых корней имеет место следующее неравенство для переходной функции системы:

, где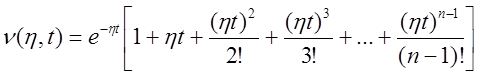

Слева – миноранта, справа – мажоранта.

Миноранта совпадает с переходной функцией, если характеристическое уравнение имеет корень  кратности n:

.

Очевидно, этот n-кратный корень по модулю равен среднегеометрическому корню: . Таким образом, при всех вещественных корнях характеристического уравнения наименьшее время переходного процесса имеет место при равенстве этих корней.

Степень быстродействия можно найти без вычисления значений корней характеристического уравнения.

          Перейдём к переменной . Смещённое уравнение:

.

В результате один или два корня попадут на ось мнимых, т.е. на границу устойчивости. Теперь можно применить любой критерий устойчивости, и определить . Так, апериодической границе устойчивости соответствует равенство нулю свободного члена

,

а колебательной границе устойчивости соответствует равенство нулю предпоследнего определителя Гурвица, прохождение годографа Михайлова через начало координат и прохождение амплитудно-фазовой характеристики разомкнутой системы через точку ().

Оценка запаса устойчивости.

При наличии пары комплексных корней  система склонна к колебаниям. Параметр  называется колебательностью. С другой стороны, комплексные корни дают в выражении для переходного процесса член вида

.

Через один период колебаний  амплитуда изменяется в  раз. Таким образом, связь колебательности с затухание за период:.