Особые точки и фазовые портреты нелинейных систем

Особые точки и фазовые портреты нелинейных систем.

Уравнения нелинейной системы второго порядка:

, .

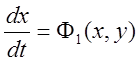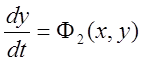Особые точки, отвечающие равновесным состояниям системы, определяются из условий , .

Для выявления типа каждой особой точки эти уравнения линеаризуются при малых отклонениях координат в окрестности особой точки. Затем определяются корни характеристического уравнения линеаризованной системы, по которым устанавливается тип особой точки.

Пример. Уравнения нелинейной системы:

, .

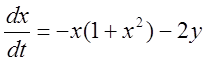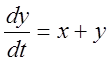Уравнение фазовых траекторий:

.

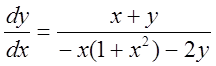Условия на особые точки:

, .

Эта система имеет три решения:

1) , 2) , 3) .

Каждому из решений соответствует равновесное состояние.

В окрестность точки () линеаризованные уравнения имеют вид:

, .

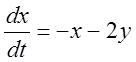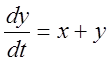Характеристическое уравнение:

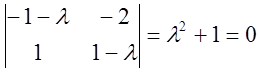. Отсюда .

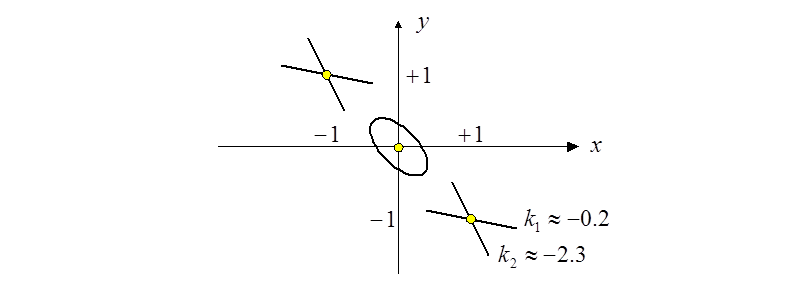
Корни чисто мнимые. Следовательно, это точка типа «центр».

В окрестности точки () вводим малые отклонения координат: . Подставляя  в исходную систему уравнений и отбрасывая нелинейные члены, получаем линеаризованную систему:

, .

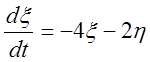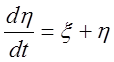Характеристическое уравнение:

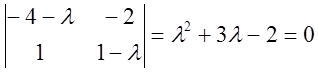. Отсюда .

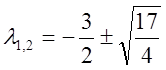Корни вещественны и имеют разные знаки. Следовательно, это точка типа «седло».

В окрестности точки (), подстановкой  в исходную систему уравнений, получаем ту же линеаризованную систему, что и в предыдущем случае. Следовательно, это тоже точка типа «седло».

Найдём асимптоты фазовых траекторий в седловых точках. Полагая , из уравнений фазовых траекторий

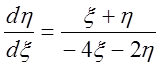 получим 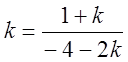, или , откуда .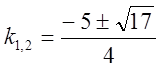

Для определения направление движения изображающей точки по фазовым траекториям достаточно взять какую-либо одну точку. Например, в точке (), согласно исходной системе, имеем . В силу непрерывности системы, в том же направлении движутся изображающие точки по соседним фазовым траекториям.

Ни одно из этих трёх равновесных состояний не является устойчивым. Методом изоклин можно уточнить ход фазовых траекторий. Уравнение изоклины

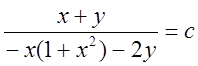 при  имеет вид: .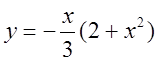

Эта кривая изоклина, соответствующая углу наклона фазовых траекторий , проходит через все особые точки. При  изоклина по-прежнему пройдёт через начало координат (особая точка), но не пройдёт через две другие особые точки.

Общие замечания.

При наличии нескольких особых точек на фазовой плоскости получаются области с различными типами фазовых траекторий. Особые кривые, разделяющие области с различными типами фазовых траекторий, называются сепаратрисами.

Существуют особые кривые другого типа – предельные циклы. Это замкнутые кривые, соответствующие периодическим процессам, в окрестности которых имеют место колебательные переходные процессы. Предельные циклы могут быть устойчивыми или неустойчивыми.

Физический смысл устойчивого предельного цикла – автоколебания системы. Причём амплитуда и частота автоколебаний не зависит от начальных условий, а определяется внутренними свойствами системы. В линейных системах собственные периодические колебания возможны только на границе устойчивости, причём амплитуда их определяется начальными условиями.

Физический смысл неустойчивого предельного цикла – граница областей начальных условий. При начальных условиях, лежащих внутри неустойчивого предельного цикла, получается затухающий переходной процесс, если же они лежат снаружи – расходящийся. Говорят: система устойчива «в малом» и неустойчива «в большом».

Таким образом, типы динамических процессов нелинейных систем могут существенно зависеть от начальных условий.