Теория рассеяния атомов и электронов достаточно подробно рассмотрена в литературе [8, 9]. В наших лекциях на нескольких простых с математической точки зрения примерах покажем возможности применения результатов исследования сечений парных столкновений для понимания физики взаимодействия частиц.
Задача о столкновении двух
частиц, как и всякая задача двух тел, сводится к задаче о рассеянии одной частицы с приведенной массой в поле ![]() неподвижного силового центра.
неподвижного силового центра.
Напомним, что волновая функция относительного движения сталкивающихся частиц представляет сумму падающей плоской волны и рассеянной расходящейся волны:
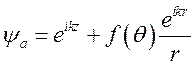 ,
(7.1)
,
(7.1)
где ![]() —
неизвестная функция угла рассеяния
—
неизвестная функция угла рассеяния ![]() между осью z и направлением движения рассеянной частицы
между осью z и направлением движения рассеянной частицы
Вероятность рассеянной
частице пройти через элемент поверхности ![]() равна
равна ![]() ,где
,где ![]() — поток рассеянных частиц и
— поток рассеянных частиц и ![]() — поток падающих частиц.
— поток падающих частиц.
Для потока частиц известно выражение
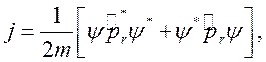 (7.2)
(7.2)
где ![]() — оператор импульса.
— оператор импульса.
Из (7.1) и (7.2) получим
![]() и
и 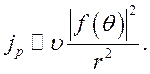 (7.3)
(7.3)
Учитывая, что ![]() , из (7.3) получим
, из (7.3) получим
![]() (7.4)
(7.4)
Таким образом, задача рассеяния
сводится к нахождению функции
![]() .
.
Мы воспользуемся борновским приближением, когда потенциальная энергия взаимодействия частиц может рассматриваться как возмущение [5]. Тогда вероятность перехода между состояниями непрерывного спектра, аналогично (2.1), дается формулой:
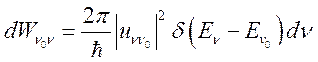 (7.5)
(7.5)
Рассматривается переход
из состояния с начальным импульсом
![]() в состояние с импульсом
в состояние с импульсом ![]() частицы, рассеянной в элемент телесного угла
частицы, рассеянной в элемент телесного угла ![]() .В качестве интервала состояний
.В качестве интервала состояний ![]() можно
взять
можно
взять ![]() - объем в импульсном пространстве,
- объем в импульсном пространстве, ![]() .
.
Волновую функцию
налетающей частицы ![]() пронормируем на равную единице плотность потока
пронормируем на равную единице плотность потока
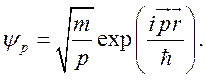 (7.6)
(7.6)
Волновую функцию рассеянной частицы ![]() , с
учетом выбранного значения
, с
учетом выбранного значения ![]() , необходимо записать в
виде
, необходимо записать в
виде
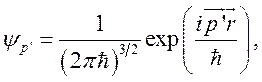 (7.7)
(7.7)
что обеспечивает
ее нормировку на ![]() -функцию в импульсном
пространстве
-функцию в импульсном
пространстве ![]() .
.
В этих условиях получим
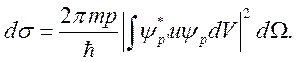 (7.8)
(7.8)
Сравнивая (7.4) и (7.8) и подставляя явные выражения для ![]() и
и ![]() , найдем
, найдем
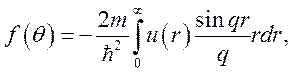 (7.9)
(7.9)
где ![]() ,
, ![]() и
и ![]() —
угол рассеяния. Здесь предположено,
что поле и — центральное.
—
угол рассеяния. Здесь предположено,
что поле и — центральное.
При ![]() в случае малых скоростей имеем
в случае малых скоростей имеем ![]() и
и
 (7.10)
(7.10)
где а — характерный размер локализация поля, т.е. рассеяние оказывается изотропным и не зависит от скорости.
В обратном предельном
случае рассеяние резко анизотропно и направлено вперед, в узком конусе с углом ![]() .
.
Для определения сечения
рассеяния нужно знать потенциал ![]() , который в общем случае может быть
представлен в виде
, который в общем случае может быть
представлен в виде
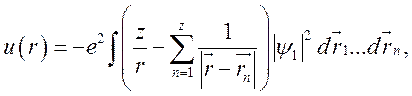 (7.11)
(7.11)
где ![]() — координаты всех электронов в атоме,
— координаты всех электронов в атоме, ![]() — волновая функция электронов в атоме.
— волновая функция электронов в атоме.
Волновая функция ![]() известна в аналитическом виде для немногих атомов. В частности, для
водорода в основном 1s состоянии имеем
известна в аналитическом виде для немногих атомов. В частности, для
водорода в основном 1s состоянии имеем
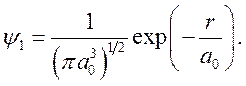 (7.12)
(7.12)
Подставляя (7.12) в (7.11) и интегрируя, получим
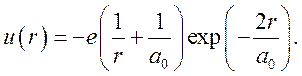 (7.13)
(7.13)
Используя (7.13) из (7.8) найдем
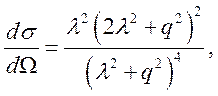 (7.14)
(7.14)
где ![]() .
.
Полное сечение упругого рассеяния электрона на атоме водорода равно
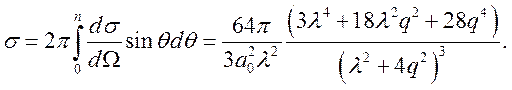 (7.15)
(7.15)
При ![]() — медленные частицы
— медленные частицы
![]() (7.16)
(7.16)
и в случае ![]()
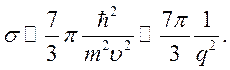 (7.17)
(7.17)
Для описания
взаимодействия между разнообразными частицами найти точное значение ![]() не удается, и в этом случае применяются различные приближенные
виды потенциала взаимодействия.
Очевидно, что критерием правильности выбора
не удается, и в этом случае применяются различные приближенные
виды потенциала взаимодействия.
Очевидно, что критерием правильности выбора ![]() является сравнение теоретического значения
является сравнение теоретического значения ![]() и полученного в эксперименте. Таким путем
удается определить
характер взаимодействия между частицами. Ниже мы приведем наиболее часто используемые приближения
и полученного в эксперименте. Таким путем
удается определить
характер взаимодействия между частицами. Ниже мы приведем наиболее часто используемые приближения ![]() .
.
1.Гладкие упругие шары
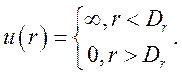 (7.18)
(7.18)
Грубое приближение, но удобное в расчетах.
2. Точечные центры притяжения или отталкивания
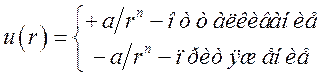 (7.19)
(7.19)
п = 1 — кулоновское взаимодействие,
п = 9 ![]() 15 — отталкивание молекул,
15 — отталкивание молекул,
п = 4 — дипольное взаимодействие между заряженной частицей и молекулой.
3. Потенциал Сазерленда
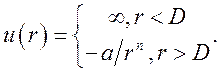 (7.20)
(7.20)
Для n = 6 этот потенциал соответствует взаимодействию Вандер — Ваальса.
4. Потенциал Ленарда — Джонса
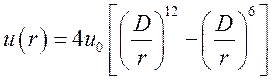 (7.21)
(7.21)
хорошо описывает взаимодействие сферических неполярных молекул.
Неупругое столкновение электрона с атомом рассмотрим с помощью борновского приближения, условие применимости которого для задач рассеяния требует, чтобы скорость падающего электрона была велика по сравнению со скоростью атомных электронов. Что касается потери энергии, то она может быть любой.
Неупругие столкновения сопровождаются изменением внутреннего состояния атома. Атом может перейти из нормального в возбужденное состояние дискретного или непрерывного спектра. Последний случай означает ионизацию.
Будем исходить из общей формулы для вероятности перехода типа (7.5):
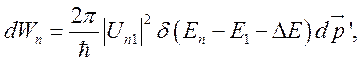 (7.22)
(7.22)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.