Определение характеристик частиц по кинематике парных столкновений (Глава 7 учебного пособия), страница 2

где , ,  — импульсы налетающего электрона до и после столкновения. и — энергии атома на первом и п-мэнергетических уровнях. — матричный элемент от энергии взаимодействия падающего электрона с атомом. Потенциал взаимодействия равен

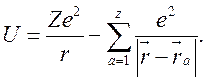                                        (7.23)

Интегрирование (7.22) по абсолютной величине  дает

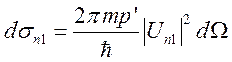                                      (7.24)

Если в матричный элемент подставить волновые функции (7.6) и (7.7), то получим

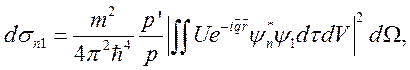                          (7.25)

где  — элемент конфигурационного пространства всех электронов атома, а элемент объема dV — определяется координатами налетающего электрона.

Отметим, что взаимодействие с ядром не вносит вклад в возбуждение в силу ортогональности и .

В выражении (7.25) возможно интегрирование по координатам налетающего электрона [5]:

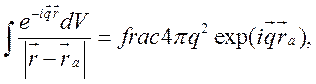                                  (7.26)

что позволяет преобразовать (7.25) к виду

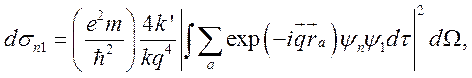                          (7.27)

где  и .

Эта формула описывает рассеяние в элементе телесного угла . Однако часто удобнее рассчитать сечение, отнесенное к элементу потери импульса dq. Учитывая, что , получим , отсюда

.

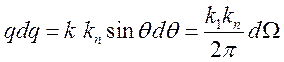Это позволяет получить выражение для сечения в виде

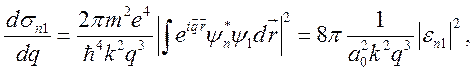                       (7.28)

где .

7.3. Неупругие столкновения быстрых электронов с атомами, возбуждение и ионизация

Электроны будем считать быстрыми, если .

Рассмотрим диапазон изменения вектора . Учитывая, что  и  при , то для быстрых электронов  и

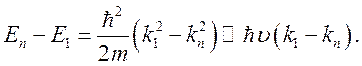                             (7.29)

Основной вклад в сечение вносит рассеяние на малые углы:

                                        (7.30)

Таким образом, минимальное значение q

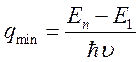                                             (7.31)

при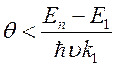

В интервале углов  имеем

                                                   (7.32)

Учитывая, что величина  порядка энергии связи атома, т.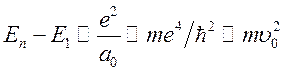е. , где  — орбитальная скорость электрона. Тогда соотношения (7.31) и (7.32) можно представить в виде

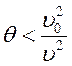 и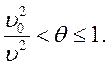

При рассеивании на малые углы  величина  может быть как больше, так и меньше единицы. Действительно,  достигается при , т.е.

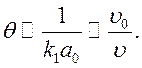
Рассмотрим случай малых q, т.е. , что соответствует случаю . Тогда  и при расчете в (7.28) первый член разложения отличен от нуля только при п = 1, т.е. описывает упругое рассеяние. Для второго члена разложения получим

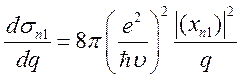                                      (7.33)

отсюда полное сечение рассеяния

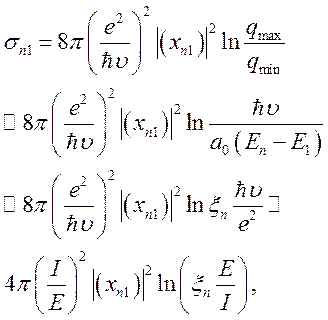                                  (7.34)

где  — безразмерная константа, зависящая от уровня п, I — потенциал ионизации атома. Для водорода: .

При  интеграл (7.28) мал, так как содержит быстро осциллирующую функцию . Большие q означают, что атому передается импульс, большой по сравнению с первоначальным импульсом атомных электронов :

 т.е.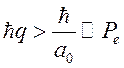

В этом случае можно рассматривать электрон атома свободным, покоящимся и использовать формулу Резерфорда.

При столкновении с большой передачей импульса оба электрона (падающий и атомный) могут приобрести сравнимые по величине скорости. В связи с этим, становятся существенными непринятые во внимание в общей формуле (7.28) обменные эффекты, связанные с тождественностью частиц. Для быстрых электронов сечение рассеяния на Z электронах атома равно

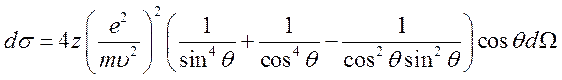               (7.35)

При столкновении частицы с энергией  с покоящейся частицей той же массы энергия частиц после столкновения равна

 

Учитывая, что из (7.35) получим

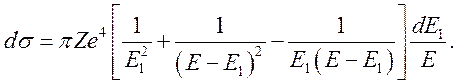                      (7.36)

Если одна из энергий или  мала по сравнению с другой, то в уравнении (7.36) существенно одно из первых двух слагаемых в скобках и формула переходит к обычной формуле Резерфорда. При  сечение убывает и играет существенную роль только при малых энергиях .

При рассеянии позитрона на атоме обменные эффекты несущественны и

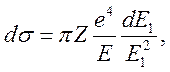                                        (7.37)

где  изменяется от I до Е.

Полное сечение равно

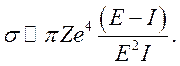                                     (7.38)

7.4. Неупругие столкновения тяжелых частиц

Рассмотрим рассеяние на атоме иона с массой М и зарядов . Рассматриваем случай, когда скорость налетающей частицы  больше скорости атомного электрона .

Тогда для сечения можно использовать общую формулу неупругого рассеяния

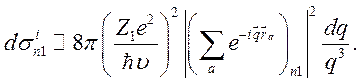                              (7.39)

Учитывая, что в данное выражение не входит масса рассеивающейся частицы, его можно использовать и для описания столкновения тяжелых частиц.

При столкновении свободных иона с электроном максимальный угол отклонения иона  Учитывая, что при больших, по сравнению с атомарными, передачах импульса электроны можно рассматривать как свободные, условие  для ионов выполняется всегда и по аналогии с (7.29) для q имеем

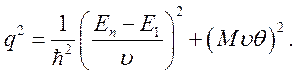                                  (7.40)

Отсюда

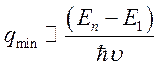                                            (7.41)

и для  получим .

Это означает, чтовся картина рассеяния на малые углы для иона оказывается суженной в отношении М/т по сравнению с рассеянием электрона.

Изменение энергии иона мало. Действительно, . Тогда . Отсюда получим

                                               (7.42)

и

.

Подставляя (7.41) и (7.42) в (7.34), для  получим

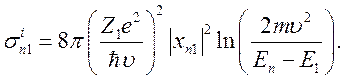                             (7.43)

В случае  из (7.39) легко найти

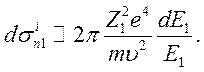                                          (7.44)

Сравнивая (7.44) и (7.37), легко увидим, что

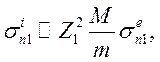
т.е. сечение возбуждения ионом при той же энергии Е в больше, чем электроном. Для однозарядных ионов (Z = 1) сечения совпадают для частиц с одинаковой скоростью.