
(Ландау, Краткий курс: Квант. мех., Глава IX)
![]() Постановка
задачи
Постановка
задачи
В целом столкновение частиц – это задача теории рассеяния частиц
![]() Классическое
рассмотрение столкновения
Классическое
рассмотрение столкновения
(Ландау, Механика)
· Система центра масс:
m – приведенная масса,
q - угол отклонения ( в СЦМ),
U(r) - поле неподвижного рассеивающего центра,
z-ось – направление движения рассеиваемой частицы.
· Формула Резерфорда
![]() Квантовомеханический
подход
Квантовомеханический
подход
·
Частица до столкновения
описывается плоской волной 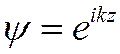 ,
,
·
Импульс 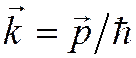 ,
,
· Рассеянная частица описывается расходящейся
сферической волной 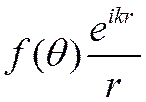 ,
,
![]() – неизвестная функция угла рассеяния q (амплитуда рассеяния), ее определение является основной задачей теории
рассеяния
– неизвестная функция угла рассеяния q (амплитуда рассеяния), ее определение является основной задачей теории
рассеяния
![]()
Сечение рассеяния
дифференциальное сечение рассеяния![]() –
–
отношение плотности рассеянных частиц к плотности падающих
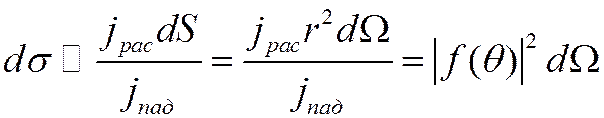 (**)
(**)
Таким образом, задача рассеяния сводится к нахождению f(q).

Изменяется только импульс микрочастицы, но не энергия
![]() Борновское
приближение: U(r)
как возмущение
Борновское
приближение: U(r)
как возмущение
![]()
![]() Воспользуемся
золотым правилом Ферми –определение вероятности перехода
Воспользуемся
золотым правилом Ферми –определение вероятности перехода ![]() между состояниями непрерывного спектра
между состояниями непрерывного спектра
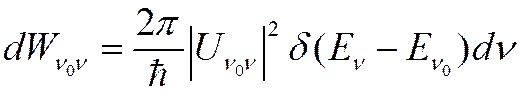 (*)
(*)
в качестве «интервала» ![]() состояний берем элемент объема
состояний берем элемент объема
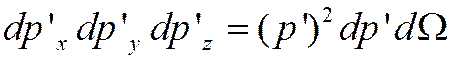
![]() ВФ
налетающей частицы пронормируем так, чтобы поток вероятности был равен единице
ВФ
налетающей частицы пронормируем так, чтобы поток вероятности был равен единице
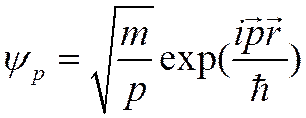 (&)
(&)
![]() Для
рассеянной частицы учтем выбранный интервал
Для
рассеянной частицы учтем выбранный интервал ![]()
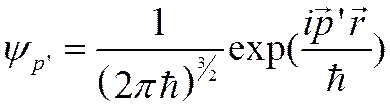 (&&)
(&&)
![]() Проинтегрировав
(*), снова получим формулу Борна
Проинтегрировав
(*), снова получим формулу Борна
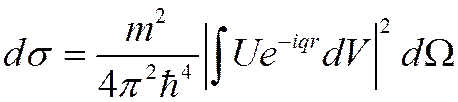 (***)
(***)
здесь введен вектор 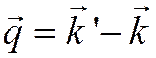 с абсолютной величиной
с абсолютной величиной
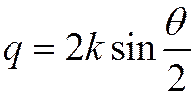
![]() Центрально-симметричное
возмущение
Центрально-симметричное
возмущение
![]() Переход к
сферическим координатам
Переход к
сферическим координатам ![]() даст
даст
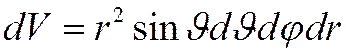 .
.
![]() Тройной
интеграл от ВФ (&) и (&&) в (***) легко преобразуется в выражение
для амплитуды рассеяния:
Тройной
интеграл от ВФ (&) и (&&) в (***) легко преобразуется в выражение
для амплитуды рассеяния:
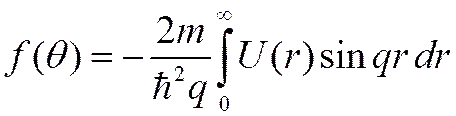 (****)
(****)
![]() Предельные случаи
Предельные случаи
Пусть а – размер локализации поля.
![]()
![]() – малые скорости,
– малые скорости,
что позволяет заменить в (****)
![]() и тогда амплитуда рассеяния
и тогда амплитуда рассеяния
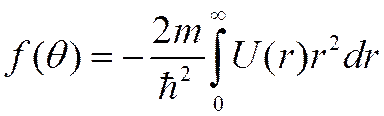
Рассеяние изотропно и не зависит от скорости (!).
![]()
![]() – большие скорости.
– большие скорости.
Рассеяние резко анизотропно и направлено вперед в узком конусе с углом
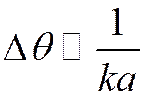
т.к. только в этом интервале углов q будет небольшой величиной, такой чтобы значение sin не осциллировало.
Вне этого конуса под интегралом (****) будет быстро осциллирующая функция умноженная на медленно меняющийся потенциал U(r) и, следовательно, среднее значение будет равно нулю.
![]()

![]()
Здесь можно использовать лабораторную систему, т.к. масса атома >> массы электрона.
![]() Потенциал
рассеивающего центра (атома)
Потенциал
рассеивающего центра (атома)
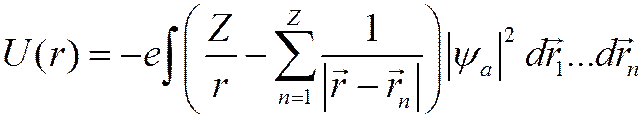 , (ÿ)
, (ÿ)
![]()
Атом водорода
![]() Однако
аналитически волновая функция
Однако
аналитически волновая функция ![]() известна лишь для
немногих атомов, в частности, для атома водорода для 1s состояния
известна лишь для
немногих атомов, в частности, для атома водорода для 1s состояния
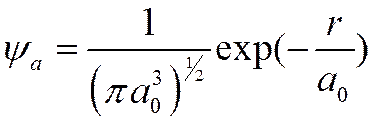
![]() Подставляя
в ÿ можно показать, что ДС в зависимости от q
определяется выражением
Подставляя
в ÿ можно показать, что ДС в зависимости от q
определяется выражением
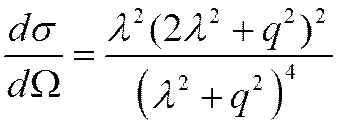 ,
,
где 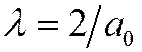 .
.
![]()
Полное (интегральное) сечение
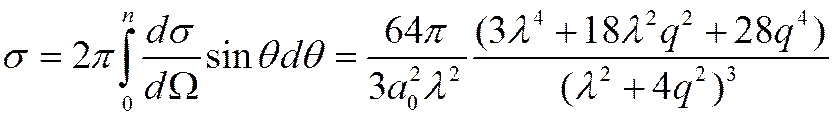
![]() Предельные случаи :
Предельные случаи :
![]()
![]() – медленные электроны
– медленные электроны
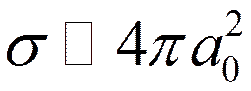
![]()
![]() – быстрые электроны
– быстрые электроны
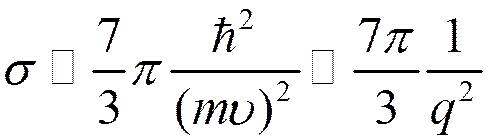
![]()
Приближенные виды (модельные потенциалы)![]()
![]()
Шары
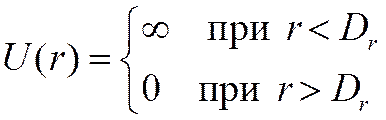
![]() Точечные центры
Точечные центры
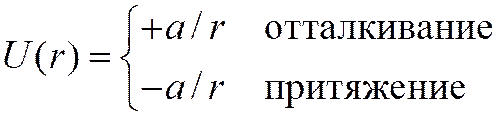
![]()
Потенциал Сазерленда
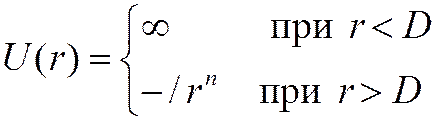
![]() Потенциал Ленарда-Джонса
Потенциал Ленарда-Джонса
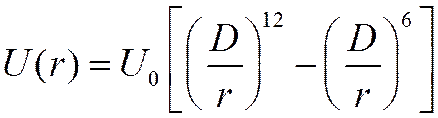
(Ландау, §148)
![]() Постановка
задачи
Постановка
задачи
![]()
![]() Борновское приближение
Борновское приближение 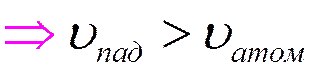
Потеря энергии – любая
![]() Атом
переходит из основного состояние в возбужденное дискретное или непрерывное
(ионизация)
Атом
переходит из основного состояние в возбужденное дискретное или непрерывное
(ионизация)
![]()
Вероятность перехода, золотое правило Ферми
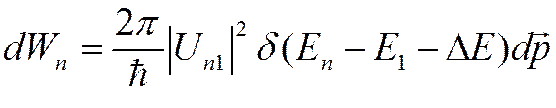 (&),
(&),
где
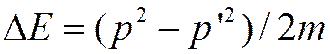
![]() Потенциальная
энергия рассеивающего центра (атома)
Потенциальная
энергия рассеивающего центра (атома)
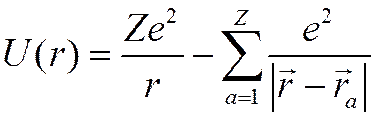
![]() Интегрирование
по модулю p’ в (&)
даст ДС с возбуждением не n-ый уровень
Интегрирование
по модулю p’ в (&)
даст ДС с возбуждением не n-ый уровень
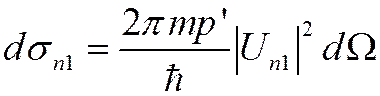
![]() Используя
волновые функции
Используя
волновые функции 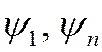 , получим
, получим
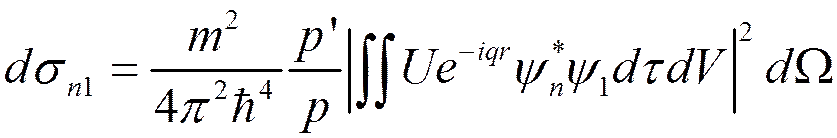 ,
,
где
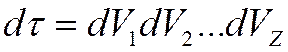 – элемент конфигурационного пространства
всех электронов атома;
– элемент конфигурационного пространства
всех электронов атома;
![]() – элемент объема, определяемый
координатами налетающего электрона
– элемент объема, определяемый
координатами налетающего электрона
![]() Можно
показать, что (Ландау III)
Можно
показать, что (Ландау III)
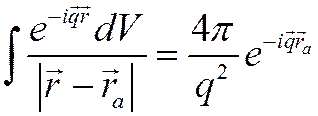
![]()
Применив это выражение, получим для ДС
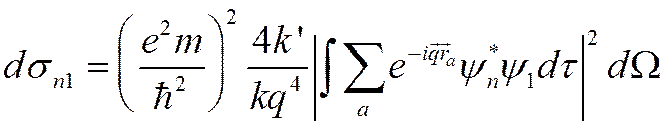
где произведены замены 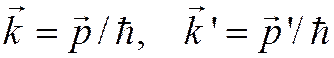 .
.
Вектор
(![]() ) – импульс, передаваемый атомному
электрону.
) – импульс, передаваемый атомному
электрону.
![]() Анализ соотношения (***)
Анализ соотношения (***)
1)
![]() малые
q, т.е.
малые
q, т.е.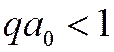 , тогда
, тогда 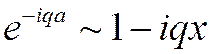
получим
![]() Полное
сечение
Полное
сечение
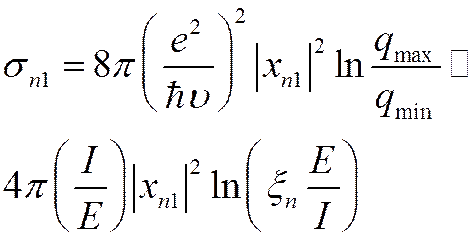
2)
![]()
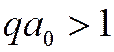 нужно учитывать обменные эффекты,
связанные с тождественностью частиц
нужно учитывать обменные эффекты,
связанные с тождественностью частиц
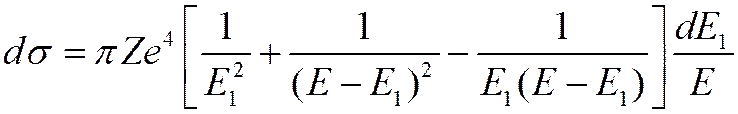
![]() Для
позитрона
Для
позитрона
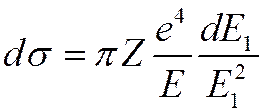
![]() Полное
сечение
Полное
сечение
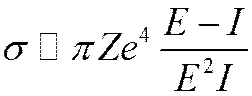

![]() Постановка задачи
Постановка задачи
ион массой М, зарядом Z
и скоростью 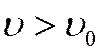 рассеивается на атоме
рассеивается на атоме
![]() Воспользуемся
общей формулой (***)
Воспользуемся
общей формулой (***)
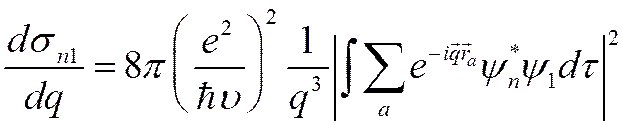
1.
![]()
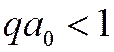
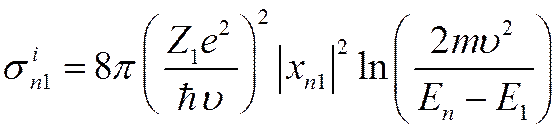
2.
![]()
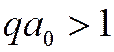
![]()
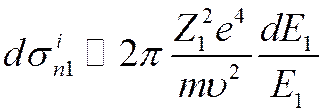
Полное сечение
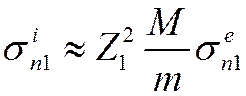
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.