Задачи на контрольной 4 ноября 2001 г. (группы 941, 942, 943, 843)
1. (300) Определить расщепление первой линии Лаймана (переход 1s® 2p) для атома водорода, помещенного в постоянное электрическое поле. Определить количество линий в разных поляризациях и величину расщепления.
Решение.
Линейный эффект
Штарка приводит к расщеплению орбиталей с главным квантовым числом n = 2. Орбитали 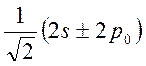 ,
2p±1 имеют энергии ±3eEa0
и 0 соответственно. Правила отбора Dl = ±1
и Dml = 0 (z),
±1
(x,y)
показывают, что первая линия Лаймана в случае z-поляризованного
света (относительно внешнего постоянного поля) расщепится на две линии
(переходы 1s ®
,
2p±1 имеют энергии ±3eEa0
и 0 соответственно. Правила отбора Dl = ±1
и Dml = 0 (z),
±1
(x,y)
показывают, что первая линия Лаймана в случае z-поляризованного
света (относительно внешнего постоянного поля) расщепится на две линии
(переходы 1s ®
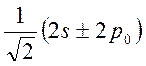 ), расстояние между которыми будет равно 6eEa0. При перпендикулярной поляризации (x,y)
линия не расщепится, так как орбитали 2p±1 не изменяют своей энергии при
включении электрического поля. Таким образом, при использовании
неполяризованного света первая линия Лаймана расщепится на три комплненты с
расстоянием между ними 3eEa0.
), расстояние между которыми будет равно 6eEa0. При перпендикулярной поляризации (x,y)
линия не расщепится, так как орбитали 2p±1 не изменяют своей энергии при
включении электрического поля. Таким образом, при использовании
неполяризованного света первая линия Лаймана расщепится на три комплненты с
расстоянием между ними 3eEa0.
2. (300) Для электронной конфигурации ln определить n, при котором основной терм имеет максимальное вырождение. Считать, что конфигурация заполнена менее чем на половину. Определить n для l = 50.
Решение. Для основного терма по первому правилу Гунда спин максимален и равен S = n/2. Поэтому мультиплетность или вырождение по спину равно (n + 1). По второму правилу Гунда для основного терма необходимо максимальное значение орбитального момента, то есть максимальное значение суммарной орбитальной проекции. Можно легко подсчитать, что Mlmax = L = nl – n(n –1)/2. Таким образом, вырождение по проекциям орбитального момента равно (2nl– n(n – 1) + 1). Общее вырождение равно
N = (n + 1)(2nl – n(n – 1) + 1).
Для нахождения максимума дифференцируем это выражение по n, приравниваем производную dN/dn нулю и находим уравнение связывающее n и l
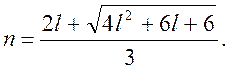
Для
l >> 1 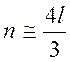 , то есть при l = 50 n » 67.
, то есть при l = 50 n » 67.
3. (500) Для атома с электронными конфигурациями np2 (основная) и np1nd1 (возбужденная) реализуется случай jj связи. Определить количество и энергии линий поглощения, которые появляются при учете спин-орбитального взаимодействия для перехода между этими конфигурациями (np2®np1nd1). Считать константы спин-орбитального взаимодействия для p и d орбиталей одинаковыми (xp = xd).
Решение. Для конфигурации np2 сильное спин-орбитальное взаимодействиев случае jj связи приведет к появлению термов (3/2, 3/2)2,0; (3/2, ½)2,1 и (1/2, ½)0 с энергиями x, -(1/2)x и -2x, соответственно. Для np1nd1 появятся термы (3/2, 5/2)4,3,2,1; (1/2, 5/2)3,2; (3/2, 3/2)3,2,1,0 и (1/2, 3/2)2,1 с энергиями (3/2)x, 0x, -x и –(5/2)x. Учитывая правила отбора DJ = 0, ±1 можно определить, что с нижнего терма (1/2, ½)0 конфигурации np2 разрешены 3 перехода в термы (3/2, 5/2)1; (3/2, 3/2)1 и (1/2, 3/2)1 возбужденной np1nd1 конфигурации. Энергии переходов равны hn + (7/2)x; hn + x и hn - (1/2)x, где hn – расстояние по энергии между конфигурациями (разность энергий p и d орбиталей). Так как константа спин-орбитального расщепления в случае jj связи велика и значительно превышает кТ, стартовать можно только с указанного выше терма конфигурации np2, ее остальные термы находятся высоко по энергии и не заселены при обычных температурах.
4. (400) Спиновая функция для четного числа N электронов имеет вид Y = ababab…abab. Определить вероятность реализации макисмального полного спина для этого спинового состояния.
Решение. При четном числе электронов все значения полного спина – целые числа, то есть все они имеют нулевую проекцию. Таким образом, общее число значений полного спина равно числу возможных комбинаций, которыми можно получить суммарную нулевую проекцию, когда половина электронов имеет проекцию a, а вторая – b. Число этих комбинаций – СNN/2. Так как для симметричной функции Y = ababab…ababреализация состояния с нулевой проекцией любого значения полного спина равновероятна, вероятность реализации единственного значения максимального спина W S = N/2 = 1/СNN/2 = ((N/2)! )2/N!.
5. (500) Определить количество расщепленых уровней (с разной энергией) и расстояние между уровнями в слабом магнитном поле для терма (3/2, 3/2)2, принадлежащего электронной конфигурации p2, для которой реализуется случай jj связи.
Решение: Терм (3/2, 3/2)2 с энергией 2x расщепляется в магнитном поле на 5 уровней, так как полный момент J = 2 имеет 5 проекций. Для определения величины расщепления необходимо определить gJ (E(MJ) = gJbHMJ) в случае jj связи. По аналогии с расчетами gJ в случае LS связи, можно определить, что в этой ситуации
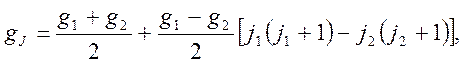
где g1 и g2 – g-факторы для 1-го и 2-го электрона, расчитанные по формулам случая LS связи. В нашей ситуации электроны p2конфигурации эквивалентны, g1 = g2 = gJ = 4/3, и расщепление между уровнями равно (4/3)*bH.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.