


Задачи на контрольной 3 ноября 2002 г. (группы 041, 042, 043)
1. (600) Определить расщепление второй линии Лаймана (переход 1s® 3p) для атома водорода, помещенного в постоянное электрическое поле. Определить количество линий в разных поляризациях и величину расщепления.
Решение.
Линейный эффект
Штарка приводит к расщеплению орбиталей с главным квантовым числом n = 3. Орбитали 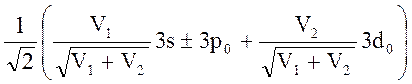 ,
,
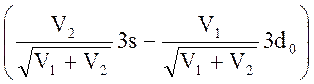 ,
, 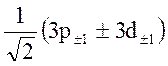 , 3d±2 имеют энергии
, 3d±2 имеют энергии ![]() , 0,
, 0, ![]() , 0, где V1,
V2, V3 – матричные элементы V3s3p0, V3p03d0 и V3p13d1, соответственно. Правила отбора Dl = ±1
и Dml = 0 (z),
±1
(x,y)
показывают, что вторая линия Лаймана в случае z-поляризованного
света (относительно внешнего постоянного поля) расщепится на две линии
(переходы 1s ®
, 0, где V1,
V2, V3 – матричные элементы V3s3p0, V3p03d0 и V3p13d1, соответственно. Правила отбора Dl = ±1
и Dml = 0 (z),
±1
(x,y)
показывают, что вторая линия Лаймана в случае z-поляризованного
света (относительно внешнего постоянного поля) расщепится на две линии
(переходы 1s ®
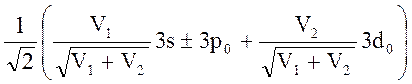 , расстояние между которыми будет равно
, расстояние между которыми будет равно ![]() . При перпендикулярной поляризации (x,y)
линия расщепится также на две линии (переходы 1s ®
. При перпендикулярной поляризации (x,y)
линия расщепится также на две линии (переходы 1s ®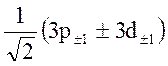 ,
расстояние между которыми будет 2V3. Таким образом, при использовании
неполяризованного света вторая линия Лаймана расщепится на четыре комплненты.
Расчет матричных элементов показывает, что
,
расстояние между которыми будет 2V3. Таким образом, при использовании
неполяризованного света вторая линия Лаймана расщепится на четыре комплненты.
Расчет матричных элементов показывает, что ![]() ,
, ![]() ,
, ![]() .
Отсюда
.
Отсюда ![]() , и внутренние две компоненты поляризованы
перпендикулярно, а две внешние параллельно.
, и внутренние две компоненты поляризованы
перпендикулярно, а две внешние параллельно.
2. (600) Определить волновую функцию с MJ = 1 мультиплета 3P1, возникшего из основного терма конфигурации p2.
Решение. Учитывая, что MJ = 1 включим в линейную комбинацию следующие микросостояния:
(1-1)aa, (-11)aa, (10)ab, (10)ba, (01)ab, (01)ba. Для нахождения коэффициентов в
линейной комбинации при этих функциях используем уравнение ![]() . Решение этого уравнения позволяет определить
искомую функцию в виде
. Решение этого уравнения позволяет определить
искомую функцию в виде
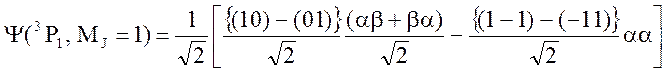 .
.
3. (200) Определить g-фактор наибольшего по энергии мультиплета, возникшего из основного терма электронной конфигурации (2k)4k.
Решение. Можно достаточно просто показать, что
основной терм этой конфигурации ![]() . Так как для него S = L
= 2k, все мультиплеты, возникшие из этого
терма имеют одинаковые g-факторы (gJ = 3/2).
. Так как для него S = L
= 2k, все мультиплеты, возникшие из этого
терма имеют одинаковые g-факторы (gJ = 3/2).
4. (200) Определить вырождение уровня с энергией +bН, который появляется из терма 2S+1L в сильном магнитном поле (эффект Пашена – Бака).
Решение. В сильном магнитном поле энергия уровней определяется выражением E = bН(ML + 2MS). Таким образом, вырождение равно числу комбинаций, которыми можно получить значение (ML + 2MS) = 1. Анализ позволяет представить следующие случаи и ответы
Целое значение S
1) при L ³ 2S+1 ответ 2S+1
2) при L < 2S+1 и при четном L ответ L, при нечетном L ответ L+1
Полуцелое значение S
1) при L ³ 2S ответ 2S+1
2) при L < 2S и при четном L ответ L+1, при нечетном L ответ L
5. (400) Имеются две слабо взаимодействующие подсистемы, каждая состоящая из двух электронов. Для первой подсистемы спиновая функция j1 = aa, для второй - j2 = bb. Определить вероятность возможных значений полного спина для системы в целом.
Решение. Вид спиновых функций показывает, что спин каждой подсистемы равен 1, поэтому полный системы может принимать значения 2, 1, 0. Обозначим начальные функции j1 = j11, j2 = j1-1, что означает принадлежность их к состоянию подсистем со спином 1 с соответствующими проекциями. Начальное состояние определяется полной проекцией равной нулю Ms = 0. Для определения вероятности реализации определенного значения полного спина необходимо найти функцию этого спина с нулевой проекцией. Тогда квадрат коэффициента перед функцией j11j1-1 и даст нам искомую вероятность. Для спина S = 2 функция с суммарной проекцией Ms = 2 может быть записана в виде y22 = j11·j11, где j11 = aa и j11 = aa. Действуя на эту функцию оператором понижения, получим функцию с суммарной проекцией Ms = 1
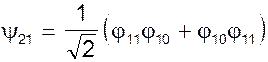 .
.
Действуя еще один раз оператором понижения, можно определить функцию с нулевой суммарной проекцией Ms = 0.
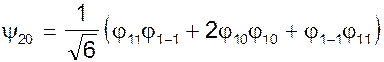 .
.
Таким образом, вероятность реализации полного спина S = 2 равна 1/6. Для полного спина S = 1 функция с проекцией M s= 1 может быть записана в виде
![]() ,
,
где коэффициенты с1 и с2 можно найти из условия ортогональности этой функции к функции y21
 .
.
При действии оператора понижения на эту функцию, получим функцию полного спина S = 1 с нулевой проекцией
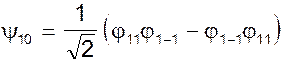 .
.
Отсюда, вероятность реализации полного спина S = 1 равна 1/2. Так как сумма вероятностей равна 1, вероятность реализации полного спина S = 0 равна 1/3. То же самое можно определить, если найти единственную функцию этого спина из условия ортогональности ее функциям y20 и y10.
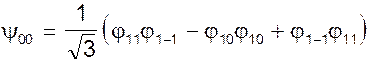 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.