Обычно попытка решить задачу о взаимосвязи константы скорости от среды в общем виде и с учетом всех возможных взаимодействий приводит к получению столь сложных уравнений, что их экспериментальная проверка невозможна. Поэтому, как правило, уравнения, связывающие константу скорости со свойствами среды, выводят на основании моделей, учитывающих ограниченное число факторов. В литературе приведено множество таких приближений (см. например [1], [2], [3]).
В данной работе мы руководствовались моделью, которая приведена в пособии [4], где для расчета влияния среды на скорость реакции была использована теория переходного состояния. Согласно этой теории, константа скорости следующим образом выражается через свободную энергию активации ΔА≠:
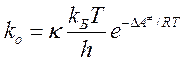
Величина ΔА≠ - разность свободных энергий активированного комплекса и исходных веществ. Сольватация может повлиять на скорость реакции изменением как свободной энергии активированного комплекса, так и свободной энергии исходных веществ. Изменение свободной энергии за счет сольватации i-частицы при переходе от газа к жидкости можно учесть, используя коэффициент активности ƒi:
ΔsА(i) = RT·lnƒi
Обозначим величину ΔА≠ для реакции в газе через ΔА≠o. Тогда для реакции между частицами А и В в жидкости:
![]()
Выражения для констант скорости реакции между А и В в газе (ko) и жидкости (k) имеют вид:
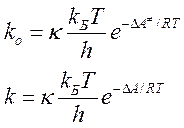
В итоге получаем уравнение Бренстеда-Бьеррума:
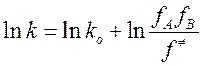
Согласно полученной формуле, задача количественного учета изменения константы скорости сводится к расчету коэффициентов активности переходного комплекса и исходных веществ.
В тех случаях, когда ионная сила раствора близка к нулю, главным фактором, влияющим на коэффициенты активности реагентов и активированного комплекса, становится диэлектрическая постоянная среды. При таком рассмотрении предполагают, что ионы имеют сферическую форму, т.е. не являются точечными зарядами. Рассмотрим частицу A с радиусом rA и зарядом ZA, ее электростатическая энергия в среде с диэлектрической проницаемостью ε равна:
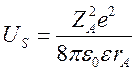
Чтобы перенести этот шар из вакуума с ε = 1 в среду, необходимо совершить работу:
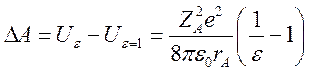
Откуда можно получить выражение для коэффициента активности частицы в растворе:
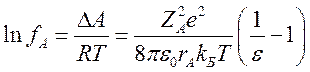
Найдем зависимость константы скорости лимитирующей стадии сольволиза (I) от диэлектрической проницаемости среды. Для упрощения рассмотрения задачи, будем исходить из предположения, что в переходном комплексе (CH3)3C+ и Cl− находятся на расстоянии, при котором возможна их эффективная сольватация молекулами растворителя, т.е. в первом приближении их можно считать свободными ионами. Следовательно, для них можно найти величины lnf описанным выше методом. Тогда:
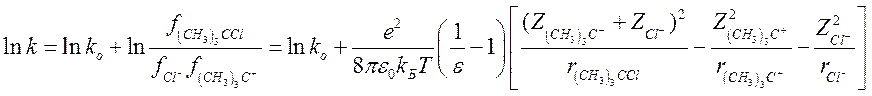
Положив ![]() , получим
, получим
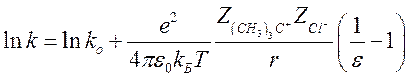 (1)
(1)
Таким образом, в данной реакции константа скорости должна
увеличиваться с ростом ε.
3. Экспериментальная часть.
Кинетику этой реакции изучали кондуктометрическим методом по изменению электропроводности раствора. В связи с высокой летучестью трет-бутилхлорида скорость реакции сильно зависит от объема газовой фазы в реакторе. Кондуктометрический метод позволяет изучать кинетику реакции в отсутствие газовой фазы и, таким образом, сразу получать истинные значения константы скорости.
Оборудование
1. Кондуктометр АНИОН 4120.
2. Персональный компьютер с установленной на нем программой для передачи данных «Dcom.exe».
3. Кондуктометрическая ячейка
Реактивы
1. Водно-спиртовые растворы с концентрациями (об. % спирта): 0; 21,5; 25,1; 30,2; 35,4; 40,7; 45,3; 49,6. Они были приготовлены следующим образом. Готовились растворы с примерным содержанием спирта (об. %) 0, 20, 25, 30, 35, 40, 45, 50. Точный состав определяли путем измерения плотности раствора ареометром и сравнением полученных данных с литературными [5].
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.