Однородное линейное уравнение. Неоднородные уравнения

          Всякое решение уравнения (6.1) является частным решением, так что особых решений оно не имеет.

          Однородное линейное уравнение (ОЛДУ)

                                                                          (6.2)

(всегда) имеет нулевое решение , удовлетворяющее нулевым начальным условиям  при  и оно единственно.

Теорема 2. Общее решение ОЛДУ есть линейная комбинация решений  его фундаментальной системы:

                                                 .                                    (6.3)

Определение 2. Фундаментальной системой решений (ФСР) уравнения (6.2) называется n его любых линейно-независимых частных решений .

Замечание. Для любого ОЛДУ существует бесконечное число фундаментальных систем решений.

Определение 3. Система из n функций  называется линейно-независимой ( на (a,b)) системой, если тождество

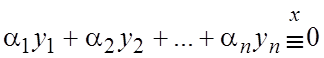                                                                                    (6.4)

выполняется лишь в случае .

Теорема 3. Чтобы система решений  была фундаментальной, необходимо и достаточно, чтобы ее определитель Вронского

                                                                             (6.5)

был отличен от нуля хотя бы в одной точке интервала .

Ниже (§10.6.2) показывается, что построить ФСР в элементарных функциях удается всегда для уравнений с постоянными коэффициентами – для этих уравнений легко находится общее решение. Для уравнений с переменными коэффициентами общего (точного) метода построения ФСР не существует.

Пример 1. Показать, что система функций  линейно независима на интервале (.

Решение. Равенство (6.4) может выполняться лишь при условии, что ; иначе в левой части будем иметь многочлен степени не выше третьей, который может обратиться в нуль не более, чем при трех значениях x из данного интервала.

Пример 2. Показать, что система функций , где  попарно различны, линейно независима на интервале .

Решение. Предположим противное; тогда в тождестве (6.4) . Пусть это . Деля обе части тождества (6.4) на , получим: . Дифференцируя это тождество и деля обе части его на , придем к тождеству . Дифференцируя, получим , что невозможно, так как  по предположению,  по условию, а .

Замечание. Для случая двух функций критерием их линейной независимости является отношение их, тождественно не равное постоянной.

Пример 3. Функции tgx и ctgx линейно независимы в интервале , так как их отношение 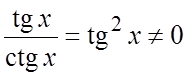 в этом интервале. Функции sin2x и  линейно зависимы в интервале , так как их отношение 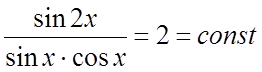 в этом интервале (в точках разрыва функции  доопределяем это отношение по непрерывности).

Пример 4. Найти определитель Вронского для функции .

Решение. Имеем

.

Пусть  есть система из n линейно-независимых на отрезке [a,b] функций, имеющих все производные до n-го порядка включительно. Тогда уравнение

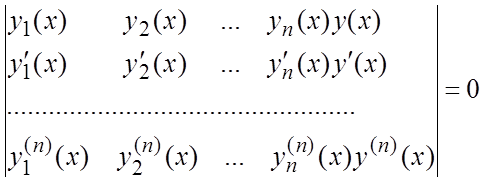                                                             (6.6)

где - независимая функция, определяет ДУ, для которого функции  составляют ФСР.

Пример 5. Составить ДУ, для которого функции 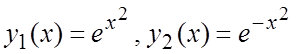 образуют ФСР.

Решение. Составим уравнение (6.6):

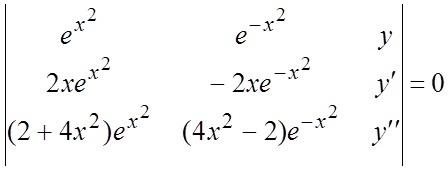 или .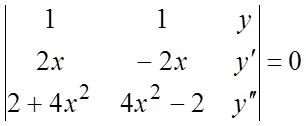

Раскрывая последний определитель по элементам третьего столбца, получим искомое уравнение: .

Замечание. В данном примере определитель Вронского  обращается в ноль при , что не противоречит общей теории, так как записав уравнение в виде 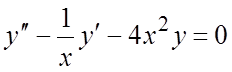, обнаружим, что коэффициент при  терпит разрыв при .

          Если известно какое-либо частное решение  уравнения (6.2), то подстановка приводит это уравнение к линейному уравнению относительно функции , не содержащему (явно) этой функции и, следовательно, подстановка  понижает порядок этого уравнения на единицу.

Пример 6. Найти общее решение уравнения , если функция  есть его частное решение.

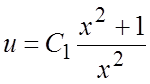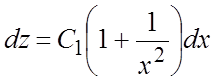Решение. Подставив  в уравнение, убеждаемся в том, что , действительно, является его частным решением. Положим , найдем . Подставив  в уравнение, после преобразования придем к уравнению . Полагая здесь , придем к уравнению первого порядка относительно функции , общее решение которого имеет вид . Учитывая, что , придем к уравнению , интегрируя которое, найдем: 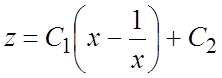. Заменяя z по формуле , получим общее решение исходного уравнения: .

Замечание 1. Изложенный метод обобщается на случай, когда известны k частных линейно-независимых решений уравнения (6.2).

Замечание 2. Для построения общего решения ОЛДУ  достаточно знать только одно ненулевое частное решение его. При этом второе частное решение  можно найти по формуле .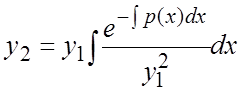

Пример 7. Найти общее решение уравнения , если оно имеет частное решение .

Решение. Найдем 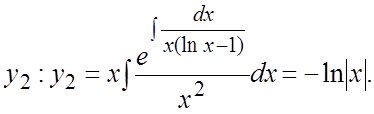 Поэтому общим решением уравнения будет .

2^°. Неоднородные уравнения (НЛДУ). Приведем теорему о структуре общего решения НЛДУ.

Теорема 4. Общее решение НЛДУ (6.1) есть сумма общего решения (6.3) ОЛДУ (6.2) и любого частного решения НЛДУ (6.1):

                                                                                        (6.7)

Все решения НЛДУ содержатся в формуле (6.7).

          Пользование формулой (6.7) на практике затруднительно, так как метод определения частного решения НЛДУ получен лишь для уравнений с постоянными коэффициентами и с правой частью некоторого специального вида.

          Приведем одно свойство решений НЛДУ (принцип суперпозиции решений): если правая часть НЛДУ (6.1) состоит из нескольких слагаемых и для НЛДУ с той же левой частью и правой частью, равной каждому из этих слагаемых в отдельности, мы можем найти частное решение, то сумма последних будет частным решением всего уравнения (6.1).