



Одномерная управляемая системы с одной степенью свободы [3].
Кинетическая
энергия системы ![]() , потенциальная энергия –
, потенциальная энергия – ![]() , добавочная неконсервативная сила –
, добавочная неконсервативная сила – ![]() .
.
Уравнение движения системы:
![]() .
.
Оператор
дифференцирования по времени (обозначение) ![]() . При
этом
. При
этом
![]() , или
, или 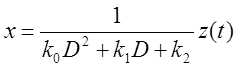 –
формальная запись.
–
формальная запись.
Передаточная функция системы (дробно-рациональная функция от D):
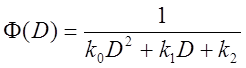 ,
, ![]() .
.
Последнее соотношение эквивалентно исходному дифференциальному уравнению. Этому соотношению ставится в соответствие структурная схема:
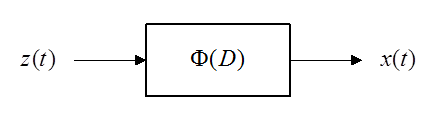 .
.
Здесь ![]() –
входной сигнал,
–
входной сигнал, ![]() – выходной сигнал.
– выходной сигнал.
Характеристическое уравнение (что это такое – ниже):
![]() .
.
Корни при условии ![]() имеют вид
имеют вид ![]() . Здесь
. Здесь
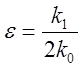 ,
, 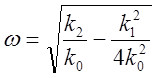 .
.
Решение уравнения движения:
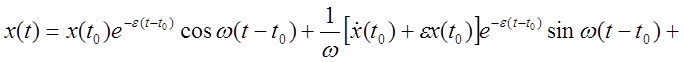
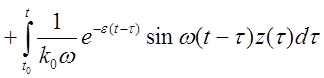 .
.
Заметим, что при ![]() ,
, ![]() (т.е.
при нулевых начальных условиях)
(т.е.
при нулевых начальных условиях)
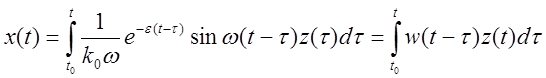 .
.
Здесь ![]() – функция
веса системы или импульсная
переходная функция данной системы:
– функция
веса системы или импульсная
переходная функция данной системы:
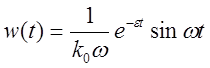 при
при ![]() ,
, ![]() при
при ![]() .
.
Заметим, что ![]() – закон движения системы при
– закон движения системы при ![]() ,
, ![]() ,
, ![]() , а также при
, а также при ![]() ,
, ![]() ,
, ![]() –
единичная импульсная функция (дельта-функция Дирака). Поэтому-то
–
единичная импульсная функция (дельта-функция Дирака). Поэтому-то ![]() и называется импульсной переходной функцией.
и называется импульсной переходной функцией.
Реакция системы на возмущение при нулевых начальных условиях:
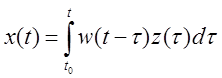 – интеграл Дюамеля-Карсона.
– интеграл Дюамеля-Карсона.
Установившийся процесс.
Пусть ![]() . Тогда закон движения системы (при нулевых
начальных условиях):
. Тогда закон движения системы (при нулевых
начальных условиях):
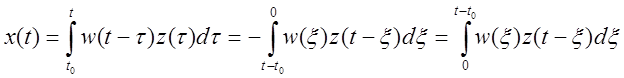 .
.
Пусть ![]() (т.е.
входной сигнал подан бесконечно давно). Тогда
(т.е.
входной сигнал подан бесконечно давно). Тогда
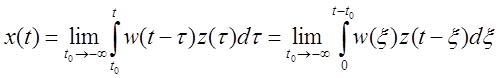 .
.
Или, для краткости, 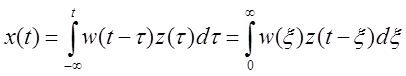 – установившийся процесс.
– установившийся процесс.
Функция веса и передаточная функция.
Стационарная система – система, описываемая линейными дифференциальными уравнениями с постоянными коэффициентами.
Изображение
функции ![]() по Лапласу:
по Лапласу:
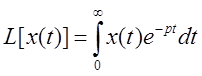 .
.
Функция
комплексного переменного ![]() , образованная из
передаточной функции
, образованная из
передаточной функции ![]() заменой
заменой ![]() ,
есть изображение по Лапласу функции веса, они полностью эквивалентны друг другу
(пока без доказательства):
,
есть изображение по Лапласу функции веса, они полностью эквивалентны друг другу
(пока без доказательства):
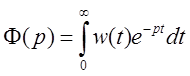 .
.
В нашем случае 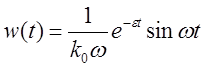 . Доказательство предыдущего утверждения:
. Доказательство предыдущего утверждения:
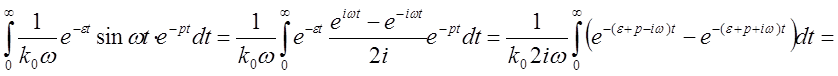
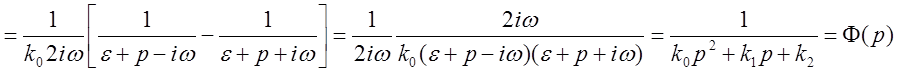 .
.
Частотная характеристика.
Обратное преобразование Лапласа даётся формулой Римана-Меллина:
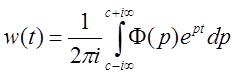 ,
, ![]() .
.
В системе, у которой все полюсы передаточной функции
расположены левее мнимой оси, собственные колебания асимптотически затухают.
Таким образом, здесь можно положить ![]() . То же касается прямого
преобразования Лапласа:
. То же касается прямого
преобразования Лапласа:
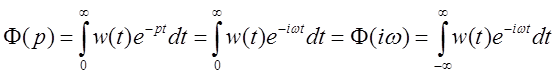 , так как
, так как ![]() при
при ![]() .
.
Функция ![]() называется частотной
характеристикой системы.
называется частотной
характеристикой системы.
Замкнутая управляемая система.
Назначение
системы – удерживать достаточно близким значение сигнала ![]() на выходе к значению сигнала
на выходе к значению сигнала ![]() на входе (обеспечивать малость
рассогласования
на входе (обеспечивать малость
рассогласования ![]() ).
).
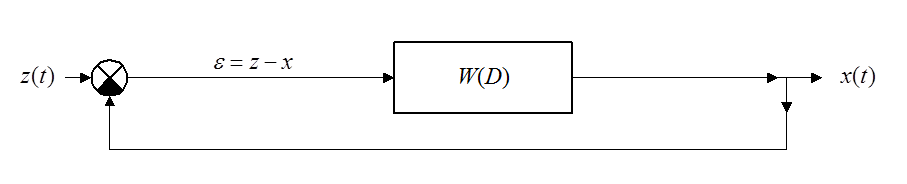
Пусть так
называемый «следящий вал» приводится во вращение двигателем постоянного тока.
Управляющее двигателем напряжение пропорционально рассогласованию ![]() , где
, где ![]() – угол
поворота задающего диска, движение которого должен повторять следящий вал.
– угол
поворота задающего диска, движение которого должен повторять следящий вал.
Уравнение движения (x – угол поворота вала):
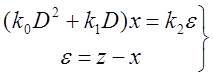
Введём обозначение 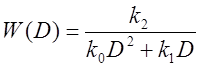 , тогда
, тогда
![]() , или
, или ![]() .
.
Уравнение замкнутой управляемой системы:
![]() , здесь
, здесь 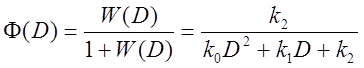 –
передаточная функция.
–
передаточная функция.
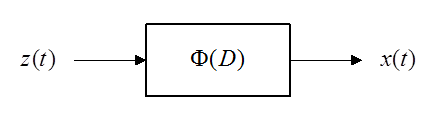
Соответствующее дифференциальное
уравнение ![]() .
.
Разомкнутая управляемая система.
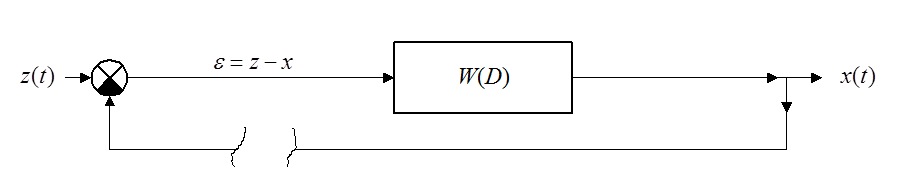
Уравнение движения:
![]() .
.
Теперь ![]() – уравнение разомкнутой управляемой
системы, а
– уравнение разомкнутой управляемой
системы, а ![]() – передаточная функция разомкнутой
управляемой системы.
– передаточная функция разомкнутой
управляемой системы.
Зависимость между передаточными функциями замкнутой и разомкнутой управляемых систем:
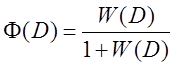 .
.
Воспроизведение преобразованного входного сигнала.
Если
управляемая система должна воспроизводить не сам входной сигнал, а
преобразованный сигнал ![]() , то следует поместить
в цепь обратной связи устройство с передаточной функцией
, то следует поместить
в цепь обратной связи устройство с передаточной функцией ![]() .
.
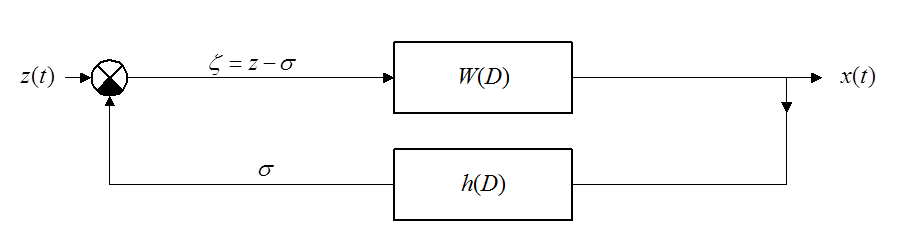
Сигнал рассогласования: ![]() .
.
Уравнения замкнутой управляемой системы:
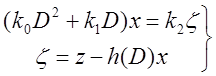 .
.
Перепишем эти уравнения так:
![]() , или
, или ![]() .
.
Передаточная функция замкнутой управляемой системы:
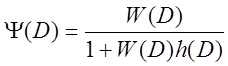 , уравнение движения
, уравнение движения ![]() .
.
Уравнения разомкнутой управляемой системы:
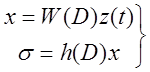 .
.
Отсюда ![]() .
.
Наконец, передаточная функция разомкнутой управляемой системы
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.