Параметр 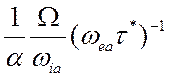 , являющийся
произведением двух рассмотренных выше параметров, определяет относительную
величину
, являющийся
произведением двух рассмотренных выше параметров, определяет относительную
величину ![]() и
и ![]() . Если
. Если 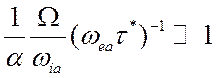 , то закон Ома принимает форму (5.25) и
форму (5.23) если
, то закон Ома принимает форму (5.25) и
форму (5.23) если 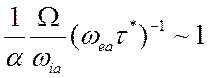 . Эти формы закона Ома
используются в магнитной гидродинамике. Если для рассматриваемой задачи имеют
место другие соотношения между определяющими параметрами, то необходимо
пользоваться той или иной формой обобщенного закона Ома, которая зависит от
относительной величины параметров (5.30).
. Эти формы закона Ома
используются в магнитной гидродинамике. Если для рассматриваемой задачи имеют
место другие соотношения между определяющими параметрами, то необходимо
пользоваться той или иной формой обобщенного закона Ома, которая зависит от
относительной величины параметров (5.30).
Уравнения магнитной гидродинамики
В этом приближении закон Ома задается в форме
![]() (5.31)
(5.31)
Заменим
в первом уравнении Максвелла (4.10) плотность тока ![]() выражением
(5.31)
выражением
(5.31)
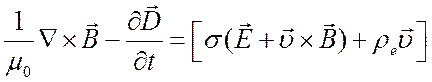 . (5.32)
. (5.32)
Оценим порядки величин входящих сюда членов, с учетом третьего уравнения Максвелла (4.10)
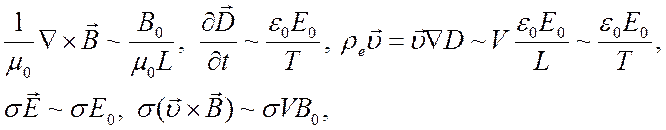
где
![]() - характерные
величины для магнитного и электрического полей, скорости, линейного размера и
времени, при этом
- характерные
величины для магнитного и электрического полей, скорости, линейного размера и
времени, при этом 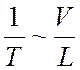 . Если величина
. Если величина ![]() такова, что имеют место неравенство
такова, что имеют место неравенство
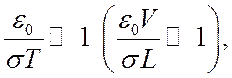 (5.33)
(5.33)
то
в равенстве (5.32) членами ![]() и
и ![]() можно пренебречь по сравнению с членом
можно пренебречь по сравнению с членом ![]() . Условие (5.33) справедливо для
большинства задач технической магнитной гидродинамики. Подставим следующие
типичные численные значения:
. Условие (5.33) справедливо для
большинства задач технической магнитной гидродинамики. Подставим следующие
типичные численные значения: ![]() и тогда получим, что
и тогда получим, что 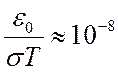 . Отношение
. Отношение 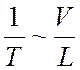 можно
трактовать как характерную частоту, равную обратному времени прохождения
средней характерной длины и приближение (5.33) носит еще название низкочастотного
приближения.
можно
трактовать как характерную частоту, равную обратному времени прохождения
средней характерной длины и приближение (5.33) носит еще название низкочастотного
приближения.
В этом случае
![]() , (5.34)
, (5.34)
первое уравнение Максвелла запишется:
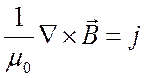 , (5.35)
, (5.35)
а выражение (5.32) можно переписать в виде
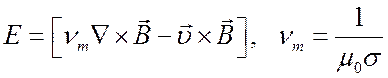 . (5.36)
. (5.36)
Величина
![]() имеет такую же размерность, как
кинематическая вязкость и называется магнитной вязкостью. Подставляя
(5.36) во второе уравнение Максвелла получим
имеет такую же размерность, как
кинематическая вязкость и называется магнитной вязкостью. Подставляя
(5.36) во второе уравнение Максвелла получим
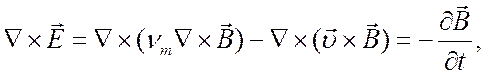
или
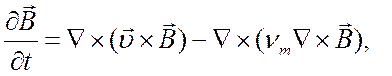 . (5.37)
. (5.37)
Уравнение (5.37) называется уравнением индукции и является одним из основных уравнений магнитной гидродинамики.
Оценивая порядки членов в уравнении индукции, можно прийти к выводу, что если
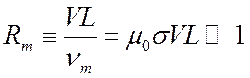 ,
,
то последним членом в правой части уравнения (5.37) можно пренебречь, и уравнение принимает вид
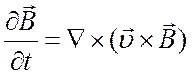 . (5.38)
. (5.38)
Безразмерная
величина ![]() , составленная из размерных величин
аналогично числу Рейнольдса, но с использовании магнитной вязкости вместо
обычной, называется магнитным числом Рейнольдса.
, составленная из размерных величин
аналогично числу Рейнольдса, но с использовании магнитной вязкости вместо
обычной, называется магнитным числом Рейнольдса.
С помощью уравнений (5.35) и (5.36) вклад электромагнитного поля в систему определяющих уравнений (4.8) может быть сведен к расчету напряженности магнитного поля на основе уравнения индукции (5.37).
Безындукционное приближение
Представим
себе, что электропроводный газ движется во внешнем постоянном магнитном поле с
индукцией ![]() и за счет движения в нем индуцируется поле
и за счет движения в нем индуцируется поле
![]() . Тогда согласно уравнению (5.35) имеем
. Тогда согласно уравнению (5.35) имеем
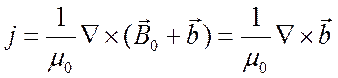 . (5.39)
. (5.39)
Проведя обезразмеривание
выражения (5.39) с масштабом тока ![]() , получим:
, получим:
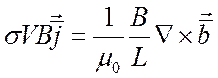
или
![]() (5.40)
(5.40)
Отсюда видно, что если
магнитное число Рейнольдса ![]() , то малый ток вызывает
сильное индуцированное поле. С другой стороны, если
, то малый ток вызывает
сильное индуцированное поле. С другой стороны, если ![]() , то
умеренной величины токи вызывают слабые индуцированные поля, которые можно
рассматривать как малые возмущения приложенного поля и в первом приближении ими
можно пренебречь.
, то
умеренной величины токи вызывают слабые индуцированные поля, которые можно
рассматривать как малые возмущения приложенного поля и в первом приближении ими
можно пренебречь.
Рекомендуемая литература по курсу лекций
1. Д.А. Франк-Каменецкий. Лекции по Физике Плазмы. М.: Атомиздат. 1964.
2. М. Митчнер, Ч. Кругер. Частично ионизованные газы. М.: «Мир». 1976.
3. А.Г. Куликовский, Г.А. Любимов. Магнитная гидродинамика. М.: «ФМ». 1962.
4. Дж. Саттон, А. Шерман. Основы технической магнитной газодинамики. М.: «Мир». 1968.
5. Л.П. Кудрин. Статистическая физика плазмы. М.: Атомиздат. 1974.
6. А.Б. Ватажин, Г.А. Любимов, С.А. Регирер. Магнитогидродинамические течения в каналах. М.: «Наука». 1970.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.