Лекция 5
Обобщенный закон Ома
Изуравнений (4.28) - (4.30) можно получить соотношение, связывающее плотность тока с другими величинами (обобщенный закон Ома). Прежде чем выводить это соотношение, оценим в этих уравнениях члены, содержащие производные.
Будем
предполагать, что характерное время задачи много больше времени между
столкновениями частиц и что скорость компонент относительно центра масс
(диффузионная скорость) мала по сравнению с хаотическими скоростями частиц,
принадлежащих данной компоненте. Если Т -
характерное время задачи, L -
характерный размер и ![]() - характерная скорость
- характерная скорость ![]() , то
эти предположения равносильны следующим:
, то
эти предположения равносильны следующим:
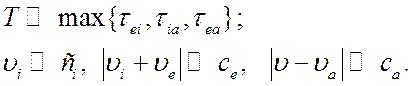 (5.1)
(5.1)
Здесь
![]() - хаотические
скорости ионов, электронов и нейтральных частиц, причем если состояние
равновесное (все температуры равны), то
- хаотические
скорости ионов, электронов и нейтральных частиц, причем если состояние
равновесное (все температуры равны), то
![]() .
.
Так как давление пропорционально произведению массовой плотности частиц на средний квадрат хаотической скорости то при условиях (5.1) членами
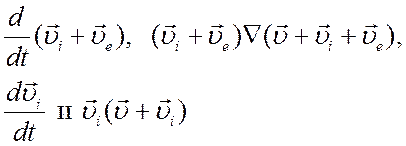
в левых частях уравнений (4.28) и (4.29) можно пренебречь по сравнению с членами в правых частях этих же уравнений.
Кроме того, в силу уравнения (4.30), при условиях (4.20), (4.23) и (4.27) имеет место соотношение
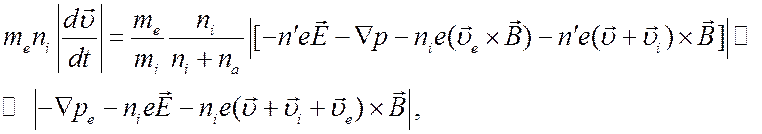
т.е.
членом 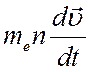 в левой части уравнения (4.28) тоже можно
пренебречь. Таким образом, при условии (5.1) уравнения (4.28)- (4.30) примут
вид
в левой части уравнения (4.28) тоже можно
пренебречь. Таким образом, при условии (5.1) уравнения (4.28)- (4.30) примут
вид
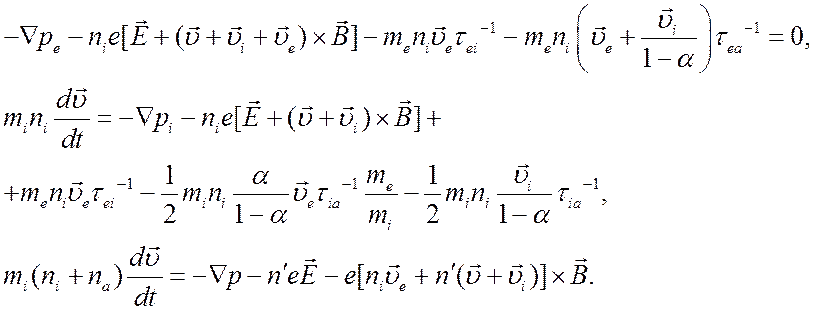 (5.2)
(5.2)
Введем следующие обозначения:
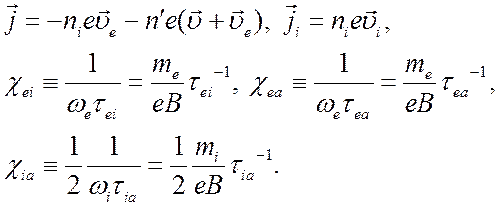 (5.3)
(5.3)
В обозначениях (5.3) при условиях (4.20) и (4.27) уравнения (5.2) примут вид:
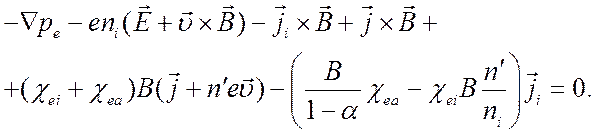 (5.4)
(5.4)
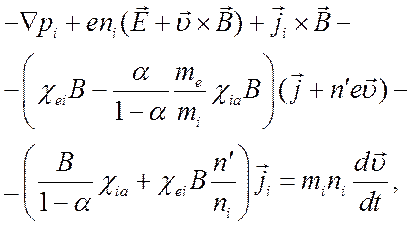 (5.5)
(5.5)
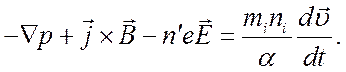 (5.6)
(5.6)
Складывая
уравнения (5.4) и (5.5) и, исключая из результата ![]() , при
помощи (5.6), получим выражение для
, при
помощи (5.6), получим выражение для ![]()
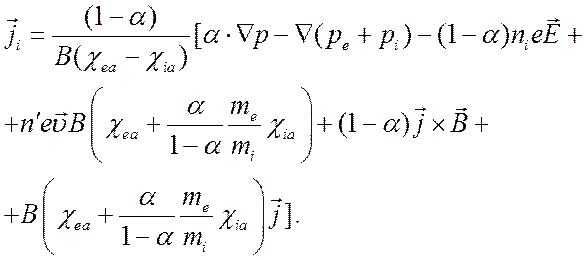 (5.7)
(5.7)
С
помощью уравнения (5.7) исключим ![]() из уравнения (5.4)
из уравнения (5.4)
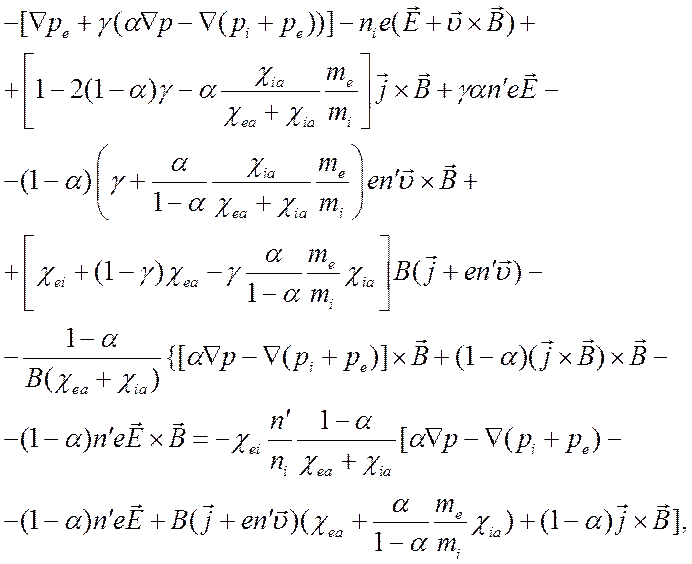 (5.8)
(5.8)
где
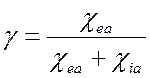 .
.
Соотношение (5.8) связывает плотность тока с напряженностью электромагнитного поля и параметрами, характеризующими среду и ее движение и его можно рассматривать как обобщенную форму закона Ома для частично ионизованных газов.
Если
скорости хаотического движения велики по сравнению с относительными
диффузионными скоростями движения компонент, то время между столкновениями
определяются хаотическими скоростями (![]() . Так
как в равновесном состоянии электроны и ионы обладают сравнимой кинетической
энергией хаотического движения, а длина свободного пробега иона
. Так
как в равновесном состоянии электроны и ионы обладают сравнимой кинетической
энергией хаотического движения, а длина свободного пробега иона ![]() меньше длины свободного электрона
меньше длины свободного электрона ![]() , то
, то
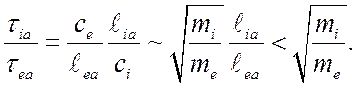
В силу (4.20) отсюда следует, что
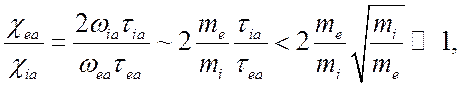 (5.9)
(5.9)
т.е.
электроны между двумя столкновениями с нейтральной частицей проходят
значительно больше витков по винтовой траектории, чем ионы. При этом ![]() , и соотношение (5.8) упрощается:
, и соотношение (5.8) упрощается:
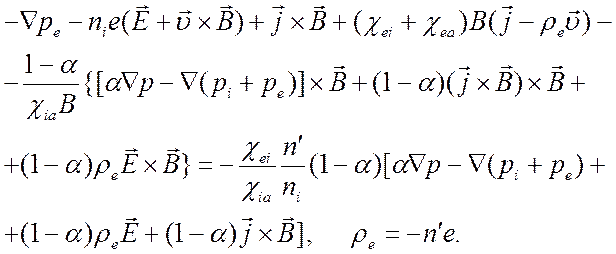 (5.10)
(5.10)
В правой части уравнения (5.10) опущены члены, малые в силу (4.20), (4.27) и (5.9). Членами, стоящими в правой части уравнения (5.10) можно пренебречь в силу (4.27), по отношению к соответствующим членам в левой части этого уравнения, если выполняется соотношение
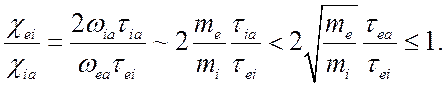 (5.11)
(5.11)
![]() может быть больше
может быть больше ![]() благодаря
далеким столкновениям между заряженными частицами. Для не очень разреженных
газов при умеренных температурах справедливо соотношение (5.11), и обобщенный
закон Ома имеет вид
благодаря
далеким столкновениям между заряженными частицами. Для не очень разреженных
газов при умеренных температурах справедливо соотношение (5.11), и обобщенный
закон Ома имеет вид
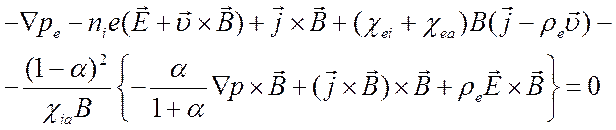 (5.12)
(5.12)
Различные формы обобщенного закона Ома
Прежде
всего, отметим, что для полностью ионизованного газа ![]()
![]() . Кроме того, из формулы (4.26) следует,
что
. Кроме того, из формулы (4.26) следует,
что 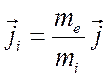 , т.е. при
, т.е. при ![]() величины
величины
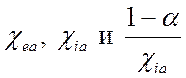 стремятся к нулю, и закон Ома принимает
вид
стремятся к нулю, и закон Ома принимает
вид
![]() . (5.13)
. (5.13)
Если газ частично ионизован, но
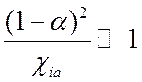 , (5.14)
, (5.14)
то 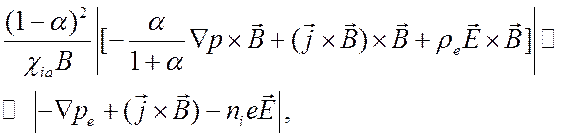 (5.15)
(5.15)
и, следовательно, закон Ома для частично ионизованного газа при условии (5.15) совпадает с законом Ома для полностью ионизованного газа (5.13) с точность до коэффициента при плотности тока.
Если электромагнитное поле оказывает существенное влияние на движение среды (именно такие задачи представляют наибольший практический интерес), то электромагнитные силы имеют порядок величины сил инерции
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.