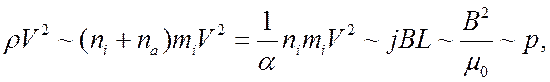 (5.16)
(5.16)
![]() - характерные
длина и скорость задачи. Соотношение (5.16) показывает, что при любой степени
ионизации
- характерные
длина и скорость задачи. Соотношение (5.16) показывает, что при любой степени
ионизации
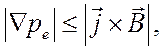 (5.17)
(5.17)
причем
![]() не существенен при малой степени
ионизации. Если скорость электронного газа относительно ионного много меньше
характерной скорости задачи
не существенен при малой степени
ионизации. Если скорость электронного газа относительно ионного много меньше
характерной скорости задачи
![]() (5.18)
(5.18)
то имеет место соотношение
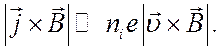 (5.19)
(5.19)
Соотношению (5.19) можно придать более обозримый вид, если воспользоваться (5.16) :
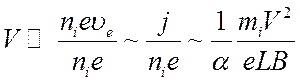
или
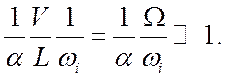 (5.
20)
(5.
20)
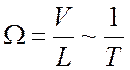 - характерная
частота задачи (Т - характерное время).
Условие (5.18) равносильно предположению о том, что циклотронная частоту ионов
- характерная
частота задачи (Т - характерное время).
Условие (5.18) равносильно предположению о том, что циклотронная частоту ионов ![]() больше характерной частоты задачи. Если
имеет место неравенство
больше характерной частоты задачи. Если
имеет место неравенство
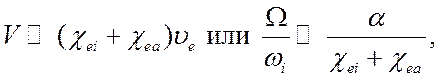 (5.21)
(5.21)
то
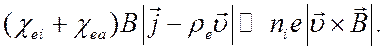 (5.22)
(5.22)
При выполнении неравенств (5.14) и (5.20) закон Ома будет иметь вид, обычно используемый в магнитной гидродинамике:
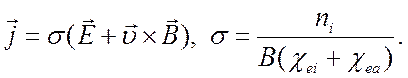 (5.23)
(5.23)
Если
определить время между столкновениями электронов ![]() с ионом
или нейтральной частицей по формуле
с ионом
или нейтральной частицей по формуле
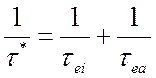 (5.24)
(5.24)
(частота столкновений равна сумме частот столкновений разного рода), то для проводимости получим формулу
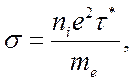
совпадающую по форме с формулой для проводимости полностью ионизованного газа.
Если кроме неравенств (5.14) и (5.20) имеет место неравенство (5.21), то закон Ома сводится к соотношению
![]() . (5.25)
. (5.25)
Это соотношение используется при изучении движений бесконечно проводящих сред.
Относительная
величина членов ![]() определяется числом
определяется числом ![]()
Если
![]() (5.26)
(5.26)
то имеет место соотношение
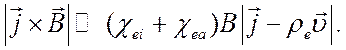 (5.27)
(5.27)
Наконец, при выполнении неравенства
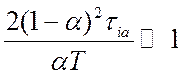 (5.28)
(5.28)
имеет место соотношение
 (5.29)
(5.29)
Таким образом, относительная величина членов в уравнении (5.12), представляющем собой обобщенный закон Ома, определяется величиной следующих безразмерных параметров:
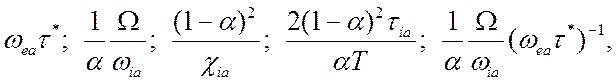 (5.30)
(5.30)
связанных как с физическими свойствами среды, так и с условиями рассматриваемой задачи.
Параметр
![]() , характеризующий спиральный пробег
электрона между двумя столкновениями определяет относительную величину членов
, характеризующий спиральный пробег
электрона между двумя столкновениями определяет относительную величину членов 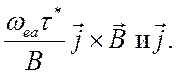 При давлении 1 атм, температуре ~
104 K и умеренных магнитных полях (B
~1 Тл) этот параметр мал и членом
При давлении 1 атм, температуре ~
104 K и умеренных магнитных полях (B
~1 Тл) этот параметр мал и членом 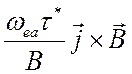 можно пренебречь.
Однако при тех же температурах и полях, но при давлении ~
можно пренебречь.
Однако при тех же температурах и полях, но при давлении ~ ![]() , величина
, величина ![]() становится
~ 1 и член
становится
~ 1 и член 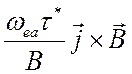 становится существенным. При
этом имеет место явление «анизотропии проводимости» газа.
становится существенным. При
этом имеет место явление «анизотропии проводимости» газа.
Параметр 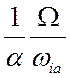 определяет
относительную величину членов
определяет
относительную величину членов 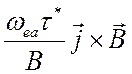 и
и ![]() . При температурах меньших
. При температурах меньших ![]() , в широком диапазоне давлений степень
ионизации
, в широком диапазоне давлений степень
ионизации ![]() мала, параметр велик
мала, параметр велик 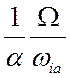 и член
и член 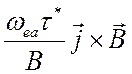 значительно
больше
значительно
больше ![]() . Если ввести в газ легко ионизующуюся
присадку, например, соли щелочных металлов, результат становится обратным. При
более высоких температурах это же явление имеет место и для «чистых» газов.
. Если ввести в газ легко ионизующуюся
присадку, например, соли щелочных металлов, результат становится обратным. При
более высоких температурах это же явление имеет место и для «чистых» газов.
Параметр, 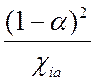 , определяющий
относительную величину членов
, определяющий
относительную величину членов 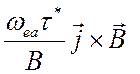 и
и 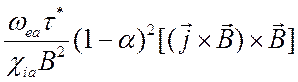 , может стать сравнимым с 1 только для
разреженных газов, движущихся в сильных магнитных полях (когда не только
электроны, но и ионы обладают спиральным пробегом). При умеренных полях и
температурах этот параметр для плотных сред всегда меньше единицы.
, может стать сравнимым с 1 только для
разреженных газов, движущихся в сильных магнитных полях (когда не только
электроны, но и ионы обладают спиральным пробегом). При умеренных полях и
температурах этот параметр для плотных сред всегда меньше единицы.
Параметр 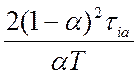 , определяющий
относительную величину членов
, определяющий
относительную величину членов 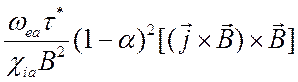 и
и ![]() , в силу условия (5.1), может стать
сравнимым с 1 только при очень низкой ионизации газа.
, в силу условия (5.1), может стать
сравнимым с 1 только при очень низкой ионизации газа.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.