Молекулы. Типы химических связей. Орбиталь, страница 3

Связь (отдельная, единичная) между атомами образуется при взаимодействии только двух электронов с противоположными спинами, принадлежащих различным атомам.

Валентность атома - это число неспаренных электронов, которые способны создать подобную связь.

Одноэлектронные молекулярные состояния

Метод самосогласованного поля Хартри – Фока, как наиболее последовательный и высоко наглядный, является в настоящее время доминирующим способом определения одноэлектронного приближения, весьма продуктивного для решения многих задач, например при определении равновесной структуры молекул в основном состоянии. Однако, последовательное изложение его применительно к молекулам достаточно объемно и, к тому же, практически не отличается по физическим представлениям изложенным ранее при изучении одноэлектронного приближения многоэлектронных атомов.

Воспользуемся другими традиционно используемыми приближениями.

Состояние отдельного электрона в двухатомной молекуле можно задать четырьмя квантовыми числами:

  m_l , (обозначается l)            проекцией орбитального момента электрона на ось молекулы,

l	0	1	2
Символ		p

   m_s = ±1/2         проекцией его спина на это направление,

  n               главным квантовым числом электрона, исходного «атома»

         орбитальным квантовым числом электрона исходного «атома»

Квантовые числа n соответствуют состоянию электрона:

►  либо в одном из атомов, когда междуатомного расстояния R → ¥ «разъединенный» атом. Состояния обозначаются  (напр.:  )

►  либо в «объединенном» атоме, при R →0; обозначение:(напр.:)

Четность. Для гомоядерной молекулы состояние отдельного электрона характеризуется свойством симметрии (инверсия): четные g состояния 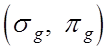 и нечетные u - состояния . Четность электронного состояния определяется четностью орбитального квантового числа l:

.

Для гомоядерных молекул:

 к связывающим относятся следующие группы электронов (орбитали):

.

 к разрыхляющим:   - электроны.

 У молекул с разными ядрами разрыхляющие орбитали обычно обозначаются .

Как и у атома, электроны с определенным n образуют оболочку; все электроны в ней называются эквивалентными. Электроны с определенным  внутри оболочки образуют подоболочку.

Квантовые числа однозначно определяют энергию электрона в двухатомной молекуле и ВФ (одноэлектронную орбиталь).

Одноэлектронные состояния и термы

В приближении нормальной связи (Расселя-Саундерса) проекция общего момента на ось молекулы

L = å l, состояние с определенной общей проекцией называется термом

L	0	1	2
Символ	å	P	D

Обозначения термов на диаграммах:

·  нормальное состояние - буквой X перед символом терма;

·  возбужденные состояния с мультиплетностью раной мультиплетности основного состояния обозначается заглавными буквами А, В, С,...;

·  возбужденные состояния другой мультиплетности - строчными буквами a, b, c.

Примеры Основные и возбужденных состояний (термов) и и соответствующих электронных оболочек некоторых молекул (А.А.Радциг, Б.М. Смирнов, Справочник по атм. и мол. физике, атомиздат, 1980)

мол	терм	электронная конфигурация	продукты диссоциации
H2
C2
NO
He2
CH		(опечатка в книге)