Линейный и квадратичный эффекты Штарка. Свойства альтернантных p-систем. Определение стабильности p-систем: молекулы, радикалы

Теория на экзамене 15 января 2000 года, группы 741, 742, 643

1. (400) Линейный и квадратичный эффекты Штарка. (После теоретической части проиллюстрировать определением изменения энергии 1s орбитали атома водорода в однородном электрическом поле E).

Решение: В первом порядке теории возмущений DE⁽¹⁾ = <1s|-eEz|1s> = 0 из-за равенства нулю угловой части интеграла <Y₀₀|Y₁₀|Y₀₀> = 0. Во втором порядке теории возмущений в соответствии с правилами отбора

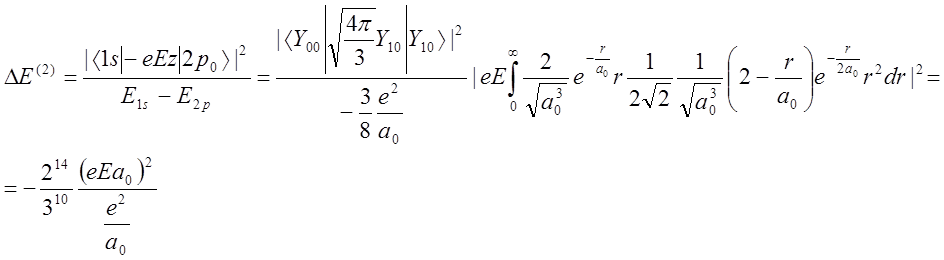Таким образом, во втором порядке теории возмущений энергия 1s-орбитали понизится за счет отталкивания от 2p₀ орбитали.

2. (300) Классификация термов и нахождение основного терма линейных молекул. (После теоретической части проиллюстрировать определением основного терма линейного радикала Н-Сl-Н).

Решение:  Основной терм радикала Н-Сl-Н - ²P_u.

3. (500) Теория представлений, неприводимые представления, таблицы характеров. (После теоретической части проиллюстрировать построением таблицы характеров для D_3d группы).

Решение: Группа D_3d - это два развернутых на 60⁰ правильных треугольника с параллельными плоскостяси и с разнесенными центрами на одной оси. После этого определения можно перечислить операции симметрии и составить таблицу характеров.

4. (400) Свойства альтернантных p-систем. (После теоретической части показать, что p-электронный заряд на всех центрах в альтернантных системах равен единице).

5. (400) Определение стабильности p-систем: молекулы, радикалы.

Задачи на экзамене 15 января 2000 года, группы 741, 742, 643

1. (200) За счет спин-орбитального взаимодействия полное расщепление терма ^2S+1L  (расстояние между мультиплетами с максимальным и минимальным значениями J) равно 14l. Определить величины S и L.

Решение: Полное расщепление равно DE = lS(2L+1). Учитывая, что L - целое число, а S - целое или полуцелое, можно определить, что S = 2 и L = 3.

2. (500) Определить расщепление уровней (функции и энергии) возбужденного состояния атома водорода с главным квантовым числом 2 в слабом внешнем магнитном поле.

Решение: Электрон может находится на 4-х вырожденных орбиталях 2s, 2p₁, 2p₀, 2p_-1. Если он находится на 2s орбитали реализуется терм ²S_1/2. При нахождении на 2p орбиталях возникают термы ²P_3/2 и ²P_1/2, функции которых легко определяются. Определение g-факторов позволяет определить расщепление этих термов в магнитном поле.

3. (300) Определить центр, на котором существует максимальная и минимальная спиновые плотности, и определить их величины для p-радикала, строение которого показано на рисунке.

Решение: На втором рисунке указана нумерация звездчатых центров. Спиновая плотность:

r₁₀ = 0,   r₉ = r₁₁ = r₁₄ = r₁₅ = r₁₆ = r₁₇ = 1/112,   r₁ = r₆ = r₇ = r₈ = r₁₂ = r₁₃ = 4/112,    r₂ = r₅ = 16/112,      r₃ = r₄ = 25/112.

4. (300) Определить разложение на неприводимые представления симметричной части прямых произведений [P´P]_s и [D´D]_s группы С_¥v.

Решение: Ниже в таблице представлены строчки характеров представлений из которых следует, что [P´P]_s = S⁺ + D и [D´D]_s = S⁺ + G. Необходимо использовать формулу 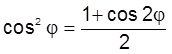. Операция R² при нахождении строчки характеров [P´P]_s и [D´D]_s для С_j равна С_2j.

5. (400) Рассмотреть предпочтительное направление присоединения атома H к пентадиенильному p-радикалу.

Решение: Направление присоединения определяется меньшей энергией оставшейся p-системы. При присоединении атома Н к первому (концевому) атому углерода остается p-система бутадиена, энергия которой равна 4a + 4.44b. Присоединение ко второму центру оставляет один изолированный p-центр и аллильный радикал, энергии которых равны 4a + 2.82b. При присоединении по центральному (третьему) атому углерода остаются две этиленовые p-системы с энергией 4a + 4b. Таким образом, присоединение наиболее эффективно по первому центру, затем по третьему и наимене эффективно по второму.