












2) Метод интегрируемых функций
По этому методу решения систем ДУ из (7.1) выделяют такое уравнение (интегрируемую комбинацию), которое можно проинтегрировать и получить первый интеграл системы. В таком случае удается понизить порядок системы. Если для системы, состоящей из n уравнений, найдено n независимых первых интегралов, то тем самым найден общий интеграл этой системы и ее интегрирование окончено.
Для нахождения
интегрируемых комбинаций иногда бывает полезно предварительно переписать данную
систему в симметрической форме (7.7) и использовать свойство равных отношений:
если 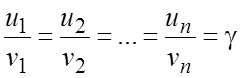 , то
, то ![]() имеет
место соотношение:
имеет
место соотношение:
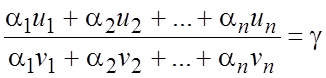 . (7.11)
. (7.11)
Числа ![]() подбираются
обычно таким образом, чтобы числитель в (7.11) был полным дифференциалом или же
знаменатель был равен нулю, или же это отношение давало интегрируемую
комбинацию.
подбираются
обычно таким образом, чтобы числитель в (7.11) был полным дифференциалом или же
знаменатель был равен нулю, или же это отношение давало интегрируемую
комбинацию.
Пример 2.
Проинтегрировать систему 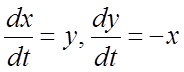 (1).
(1).
Решение.
Найдем общий интеграл методом интегрируемых комбинаций и понижения порядка
системы. Умножая почленно уравнения системы (1) соответственно на x и y и складывая
полученные уравнения, получим интегрируемую комбинацию 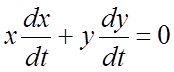 ,
откуда
,
откуда ![]() .
.
Заметим, что этот же первый
интеграл можно получить из интегрируемой комбинации 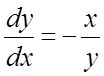 ,
которая получается из (1) делением уравнений системы. Пользуясь найденным
первым интегралом, понизим порядок системы (1) :
,
которая получается из (1) делением уравнений системы. Пользуясь найденным
первым интегралом, понизим порядок системы (1) : 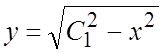 и
подставляем это значение y в первое из уравнений
системы (1):
и
подставляем это значение y в первое из уравнений
системы (1): 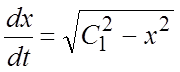 - имеем уравнение первого
порядка, интегрируя которое, находим
- имеем уравнение первого
порядка, интегрируя которое, находим 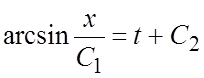 или
или 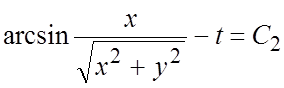 - еще один первый интеграл системы (1). Эти
интегралы независимы; опуская определение, дадим критерий независимости системы
функций
- еще один первый интеграл системы (1). Эти
интегралы независимы; опуская определение, дадим критерий независимости системы
функций ![]() ; для ее независимости требуется, чтобы
якобиан
; для ее независимости требуется, чтобы
якобиан 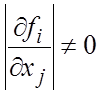 . Вычисляя якобиан, убеждаемся в независимости
первых интегралов и, таким образом, их совокупность образует общий интеграл
системы (1).
. Вычисляя якобиан, убеждаемся в независимости
первых интегралов и, таким образом, их совокупность образует общий интеграл
системы (1).
Пример 3.
Решить систему 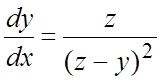 ,
, 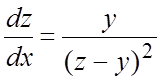 (1).
(1).
Решение.
Для нахождения интегрируемых комбинаций перепишем (1) в симметрической форме 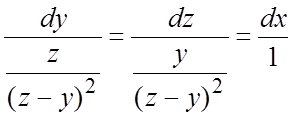 или
или 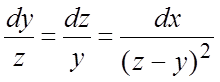 .
.
Одна из интегрируемых комбинаций:
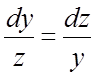 , откуда
, откуда ![]() .
Используя свойство пропорции (7.11), найдем вторую интегрируемую комбинацию:
.
Используя свойство пропорции (7.11), найдем вторую интегрируемую комбинацию: 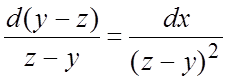 , откуда находим еще один первый интеграл:
, откуда находим еще один первый интеграл: ![]() . Совокупность их образует общий интеграл
системы (1).
. Совокупность их образует общий интеграл
системы (1).
Пример 4.
Найти общее решение системы уравнений 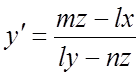 ,
, 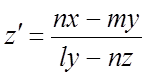 .
.
Решение. Запишем систему в симметрической форме 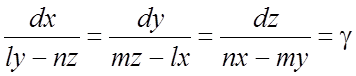 и воспользуемся соотношением (7.11).
Выбираем
и воспользуемся соотношением (7.11).
Выбираем ![]() и
и ![]() ,
получим
,
получим 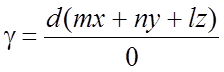 , то есть
, то есть ![]() ,
откуда
,
откуда ![]() . Аналогично, выбирая
. Аналогично, выбирая ![]() и
и ![]() , приходим
к равенству
, приходим
к равенству ![]() , откуда
, откуда ![]() . Их
совокупность неявно определяет общее решение.
. Их
совокупность неявно определяет общее решение.
Пример 5.
Найти частное решение системы 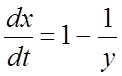 ,
, 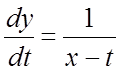 , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям: ![]() .
.
Решение.
Запишем данную систему в виде 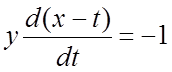 ,
, 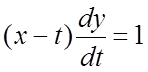 . Складывая эти уравнения, получим:
. Складывая эти уравнения, получим: 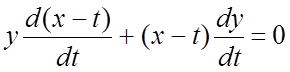 или
или ![]() .
Отсюда
.
Отсюда ![]() - первый интеграл. Так как
- первый интеграл. Так как ![]() , то второе уравнение системы примет вид:
, то второе уравнение системы примет вид: 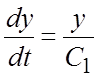 , откуда
, откуда ![]() . Таким
образом,
. Таким
образом, ![]() ,
, ![]() - общий
интеграл системы. Найдем общее решение :
- общий
интеграл системы. Найдем общее решение : 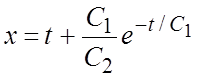 ,
, ![]() . Полагая
. Полагая ![]() в этих
равенствах, найдем
в этих
равенствах, найдем 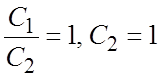 , то есть
, то есть ![]() ;
искомое частное решение:
;
искомое частное решение: ![]() ,
, ![]() .
.
Задачи для самостоятельного решения
Дифференциальные уравнения или канонические системы заменить нормальными системами дифференциальных уравнений:
247.![]() ;
248.
;
248. ![]() ; 249.
; 249.![]() ;
;
250.![]() ; 251.
; 251.![]() .
.
Проверить, являются ли функции ![]() и
и ![]() решениями
систем дифференциальных уравнений:
решениями
систем дифференциальных уравнений:
252.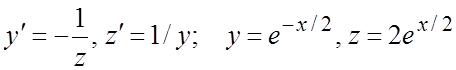 ;
;
253.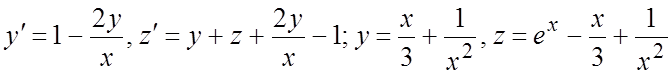 ;
;
254.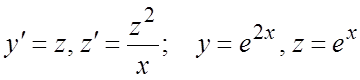 ; 255.
; 255.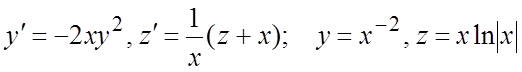 .
.
Проверить, являются ли данные функции интегралами данных систем ДУ:
256.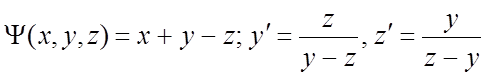 ;
;
257.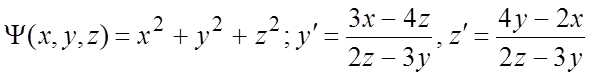 ;
;
258.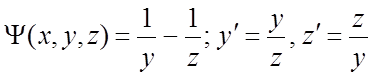 ; 259.
; 259. 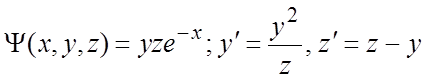 ;
;
260.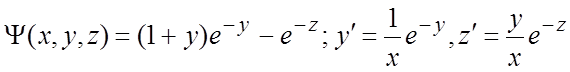 ;
;
261.a)
![]() б)
б) ![]() ;
; 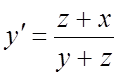 ,
, 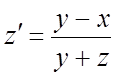 .
.
Методом исключения решить следующие системы дифференциальных уравнений:
262.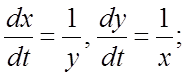 263.
263. 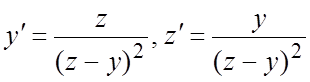 ; 264.
; 264.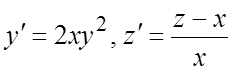 ;
;
265.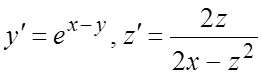 ;
266.
;
266.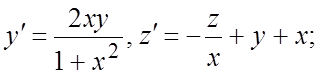
267.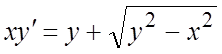 ,
, 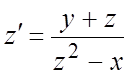 . 268.
. 268.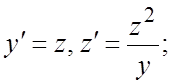 269.
269.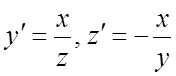 ;
;
270.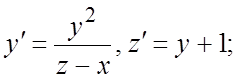 271.
271.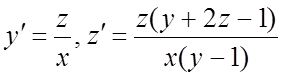 ;
;
272.![]() .
.
Методом исключения найти общее решение системы дифференциальных уравнений, выделить затем частное решение, удовлетворяющее заданным начальным условиям:
273. 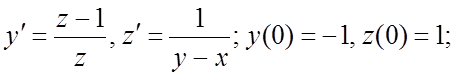 274.
274.
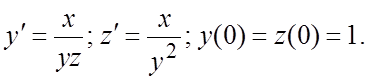
Решить системы методом интегрируемых комбинаций:
275. 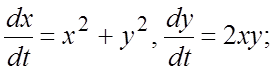 276.
276.
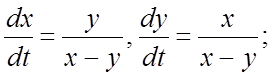
277. 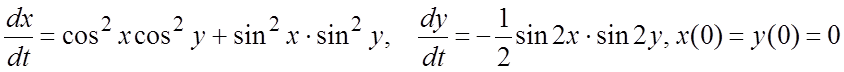 ;
;
278. 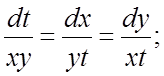 279.
279.
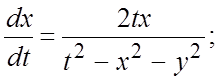
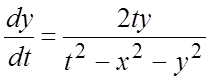 ;
;
280. 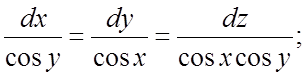 281.
281.
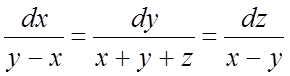 ;
;
282. 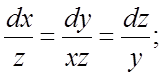 283.
283. 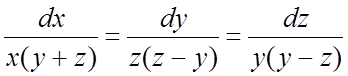 ;
;
284. 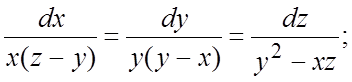 285.
285. 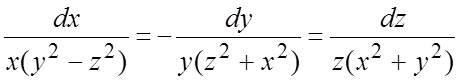 .
.
10.8. Линейные системы дифференциальных уравнений
10.8.1. Введение
1°. Однородные системы. Линейные системы (7.2) можно интегрировать общими методами, изложенными в главе 4; но для них существует специальная теория интегрирования. Введем определения.
Определение
1. Если ![]() , то система (7.2) называется однородной
линейной системой ДУ (СОЛДУ). Иначе она называется неоднородной (СНЛДУ).
, то система (7.2) называется однородной
линейной системой ДУ (СОЛДУ). Иначе она называется неоднородной (СНЛДУ).
Предполагается, что
функции ![]() и
и ![]() определены
и непрерывны в интервале (a,b).
Тогда система (7.2) имеет единственное решение, определенное во всем интервале
(a,b) и
удовлетворяющее начальным условиям (7.4). Всякое решение (7.2) является
частным, так что особых решений она не имеет.
определены
и непрерывны в интервале (a,b).
Тогда система (7.2) имеет единственное решение, определенное во всем интервале
(a,b) и
удовлетворяющее начальным условиям (7.4). Всякое решение (7.2) является
частным, так что особых решений она не имеет.
Интегрирование системы (7.2) приводит к интегрированию СОЛДУ
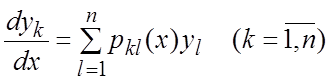 . (8.1)
. (8.1)
Система (8.1) всегда имеет
нулевое решение ![]() .
.
Оно удовлетворяет нулевым
начальным условиям ![]() при
при ![]() ; других
решений, удовлетворяющих этим условиям, нет. Чтобы построить общее решение
(8.1), достаточно знать n линейно
независимых в интервале (a,b)
частных решений:
; других
решений, удовлетворяющих этим условиям, нет. Чтобы построить общее решение
(8.1), достаточно знать n линейно
независимых в интервале (a,b)
частных решений:
![]() (8.2)
(8.2)
Такая система решений называется фундаментальной (ФСР).
Теорема 1. Для того, чтобы система решений (8.2) была фундаментальной, необходимо и достаточно, чтобы ее определитель Вронского
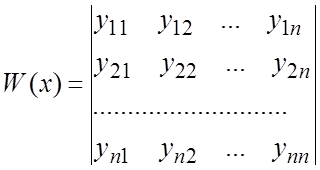 (8.3)
(8.3)
был отличен от нуля хотя бы в одной точке интервала (a,b).
Теорема 2.
При условии непрерывности коэффициентов ![]() существует
бесчисленное множество фундаментальных систем.
существует
бесчисленное множество фундаментальных систем.
Теорема 3. Линейная комбинация решений фундаментальной системы (8.2)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.