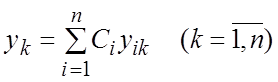 ,
(8.4)
,
(8.4)
где ![]() -
произвольно постоянные, представляет собой общее решение СОЛДУ (8.1) в области
-
произвольно постоянные, представляет собой общее решение СОЛДУ (8.1) в области
![]() . (8.5)
. (8.5)
Замечание. Все решения СОЛДУ содержатся в формуле (8.4).
2°. Неоднородные системы. Чтобы найти общее решение СНЛДУ (7.2), достаточно знать общее решение (8.4) соответствующей СОЛДУ (8.1) и одно частное решение СНЛДУ (7.2):
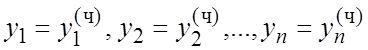 . (8.6)
. (8.6)
Теорема 3. Сумма решений (8.4) и (8.6) есть общее решение СНЛДУ (7.2) в области (8.5):
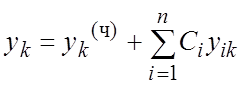
![]() .
(8.7)
.
(8.7)
Замечание.
Все решения системы (7.2) содержатся в формуле (8.7).
Метод вариации произвольных постоянных (метод Лагранжа) позволяет найти общее
решение СНЛДУ, зная лишь фундаментальную систему решения (8.2) СОЛДУ (8.1). По
этому методу решение ищем в виде
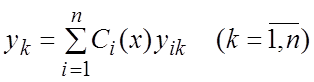 , (8.8)
, (8.8)
где ![]() -
непрерывно дифференцируемые функции от x,
подлежащие определению из системы
-
непрерывно дифференцируемые функции от x,
подлежащие определению из системы
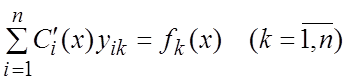 . (8.9)
. (8.9)
Решая ее алгебраически , находим ![]() , откуда квадратурами определяем
, откуда квадратурами определяем ![]() . Подставляя эти значения в (8.8), получаем
общее решение системы (7.2).
. Подставляя эти значения в (8.8), получаем
общее решение системы (7.2).
10.8.2. Линейные системы с постоянными коэффициентами
Линейная
система (7.2), у которой все коэффициенты ![]() всегда
интегрируется в квадратурах, ибо соответствующая СОЛДУ (8.1) имеет фундаментальную
систему решений, состоящую из элементарных функций. ФСР СОЛДУ строится по
методу Эйлера: решение системы (8.1) ищем в виде
всегда
интегрируется в квадратурах, ибо соответствующая СОЛДУ (8.1) имеет фундаментальную
систему решений, состоящую из элементарных функций. ФСР СОЛДУ строится по
методу Эйлера: решение системы (8.1) ищем в виде
![]() , (8.10)
, (8.10)
где ![]() и
и ![]() -
подлежащие определению величины. Подставляя (8.10) в (8.1) и сокращая на
-
подлежащие определению величины. Подставляя (8.10) в (8.1) и сокращая на ![]() , получаем систему
, получаем систему
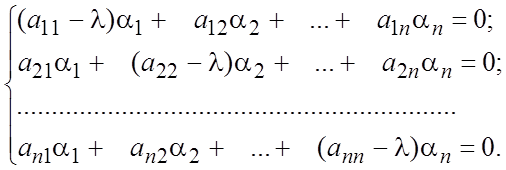 (8.11)
(8.11)
Чтобы система (8.11) имела
решение, отличное от тривиального, необходимо и достаточно , чтобы ![]() было корнем уравнения
было корнем уравнения
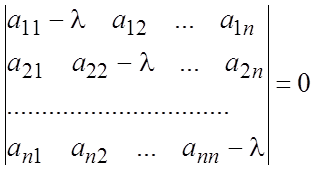 , (8.12)
, (8.12)
называемого характеристическим
уравнением. Каждому из корней (8.12) соответствует хотя бы одно частное решение
вида (8.10). Здесь возможны три случая.
1) Все корни ![]() уравнения (8.12) различны и
вещественны. Полагая в системе (8.11)
уравнения (8.12) различны и
вещественны. Полагая в системе (8.11) ![]() ,
получим систему
,
получим систему
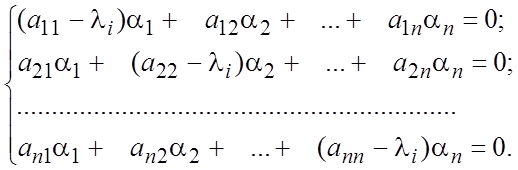 (8.11¢)
(8.11¢)
Решая ее, найдем ненулевое
решение ![]() . Подставляя
. Подставляя ![]() и
и ![]() в (8.10), найдем решение СОЛДУ, соответствующие
корню
в (8.10), найдем решение СОЛДУ, соответствующие
корню ![]()
![]() . (8.10¢)
. (8.10¢)
Построив решения, соответствующие
всем корням ![]() , получим фундаментальную систему решений
(ФСР)
, получим фундаментальную систему решений
(ФСР)
![]() . (8.2¢)
. (8.2¢)
Общее решение системы запишется в виде
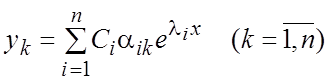 . (8.4¢)
. (8.4¢)
2) Корни характеристического
уравнения (8.12) различны, но среди них имеются комплексные. Если ![]() - корень (8.12), то
- корень (8.12), то ![]() тоже
будет корнем. Построив решение вида (8.10¢),
соответствующее корню
тоже
будет корнем. Построив решение вида (8.10¢),
соответствующее корню ![]() и отделив в нем действительную и
мнимую части, получим два вещественных линейно независимых частных решений
СОЛДУ (8.1). Построив частные решения, соответствующие всем парам комплексно
сопряженных корней и всем вещественным (если они имеются), получим ФСР (8.2¢). Общее решение запишется по формуле (8.4).
и отделив в нем действительную и
мнимую части, получим два вещественных линейно независимых частных решений
СОЛДУ (8.1). Построив частные решения, соответствующие всем парам комплексно
сопряженных корней и всем вещественным (если они имеются), получим ФСР (8.2¢). Общее решение запишется по формуле (8.4).
3) Среди корней характеристического уравнения (8.12) имеются кратные. Корню ![]() кратности k
соответствует решение вида
кратности k
соответствует решение вида
![]() , (8.13)
, (8.13)
где ![]() -
многочлены от x степени не выше k-1 (они могут вырождаться в постоянные числа), причем
среди коэффициентов всех этих многочленов k
коэффициентов произвольны, а остальные выражаются через них. Полагая поочередно
один их этих произвольных коэффициентов равным единице, а остальные равными
нулю, построим k линейно независимых частных
решений. Если
-
многочлены от x степени не выше k-1 (они могут вырождаться в постоянные числа), причем
среди коэффициентов всех этих многочленов k
коэффициентов произвольны, а остальные выражаются через них. Полагая поочередно
один их этих произвольных коэффициентов равным единице, а остальные равными
нулю, построим k линейно независимых частных
решений. Если ![]() вещественно, то эти частные
решения тоже вещественны. Если
вещественно, то эти частные
решения тоже вещественны. Если ![]() - комплексный корень,
- комплексный корень, ![]() , то
, то ![]() тоже
корень и притом той же кратности k. Определив
указанным выше методом k линейно независимых комплексных
частных решений, соответствующих корню
тоже
корень и притом той же кратности k. Определив
указанным выше методом k линейно независимых комплексных
частных решений, соответствующих корню ![]() , и
отделив в них вещественные и мнимые части, получим k
линейно независимых вещественных частных решений. Напомним, что решения,
соответствующие корню
, и
отделив в них вещественные и мнимые части, получим k
линейно независимых вещественных частных решений. Напомним, что решения,
соответствующие корню ![]() линейно зависимы с решениями,
соответствующими корню
линейно зависимы с решениями,
соответствующими корню ![]() .
.
Пример 1.
Проинтегрировать систему 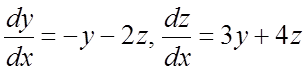 (1) по методу Эйлера.
(1) по методу Эйлера.
Решение.
Ищем частное решение системы (1) в виде (8.10): ![]() (2).
Составляем характеристическое уравнение (8.12):
(2).
Составляем характеристическое уравнение (8.12):
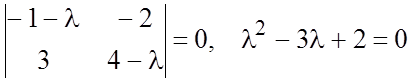 .
.
Оно имеет корни ![]() . Построим частное решение вида (2),
соответствующее корню
. Построим частное решение вида (2),
соответствующее корню ![]() . Подставляя
. Подставляя ![]() в систему (8.11¢), получим уравнение
в систему (8.11¢), получим уравнение ![]() (другое есть следствие
первого). В этом уравнении одна неизвестная – свободная неизвестная. Полагая
(другое есть следствие
первого). В этом уравнении одна неизвестная – свободная неизвестная. Полагая ![]() , получим
, получим ![]() . Таким
образом, корню
. Таким
образом, корню ![]() соответствует частное решение
соответствует частное решение ![]() . Аналогично находим частное решение,
соответствующее корню
. Аналогично находим частное решение,
соответствующее корню ![]() . Общее решение системы (1):
. Общее решение системы (1): ![]()
![]() (3). Найдем частное
решение, удовлетворяющее начальным условиям:
(3). Найдем частное
решение, удовлетворяющее начальным условиям: ![]() ,
, ![]() . Полагая в (3)
. Полагая в (3) ![]() ,
получим
,
получим ![]() ,
, ![]() ,
откуда
,
откуда ![]() и искомое частное решение:
и искомое частное решение: ![]() ,
, ![]() .
Других решений, удовлетворяющих этим начальным условиям, нет.
.
Других решений, удовлетворяющих этим начальным условиям, нет.
Пример 2. Найти общее решение системы ![]() (1).
(1).
Решение. Характеристическое уравнение
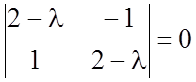 или
или ![]()
имеет корни ![]() . Строим комплексное решение,
соответствующее корню
. Строим комплексное решение,
соответствующее корню ![]() . Числа
. Числа ![]() и
и
![]() определяем из уравнения
определяем из уравнения![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.