Глава 1. Краткие основы физики плазмы
§ 4. Идеальность плазмы
По аналогии с газом плазму считают идеальной, если кинетическая энергия движения ее частиц существенно больше потенциальной энергии их взаимодействия. В газе потенциальная энергия взаимодействия частиц обусловлена силами Ван-дер-Ваальса, в плазме – кулоновским взаимодействием. Энергия кулоновского взаимодействия двух частиц с зарядом е, находящихся на расстоянии R друг от друга, равна е2/R. Среднее расстояние между частицами при плотности плазмы n составляет R~n-1/3, а кинетическая энергия частицы по порядку величины равна температуре T, измеряемой в энергетических единицах. Таким образом, условие идеальности плазмы можно сформулировать следующим образом:
![]()
е2n1/3 << T,
или
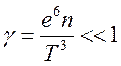 (1.8)
(1.8)
где γ так называемый параметр неидеальности [С. К. Жданов, В. А. Курнаев, М. К. Романовский, И. В. Цветков. Основы физических процессов в плазме и плазменных установках].
Этому условию можно придать и несколько иной смысл. Сечение кулоновского взаимодействия частиц определяется амплитудой рассеяния, по порядку величины равной
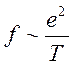
Очевидно, плазма является идеальной, если амплитуда рассеяния значительно меньше среднего межчастичного расстояния (в противном случае существенны корреляции взаимного расположения частиц)
f << R ~ n-1/3,
и вновь приходим к критерию (1.8) [С. К. Жданов, В. А. Курнаев, М. К. Романовский, И. В. Цветков. Основы физических процессов в плазме и плазменных установках].
Полезно условию идеальности плазмы придать более наглядный смысл, для этого поступим следующим образом. Выделим в объеме плазмы шар с радиусом, равным радиусу Дебая, и подсчитаем число частиц ND, содержащихся в этом шаре:
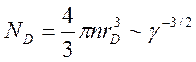 (1.9)
(1.9)
Сравнив с критерием (1.8), приходим к заключению, что плазма является идеальной, если число частиц в шаре с дебаевским радиусом велико. Часто именно число ND используется в качестве меры идеальности или неидеальности плазмы.
Проиллюстрируем полученный результат численным примером. Например, для значений температуры и плотности, типичных для термоядерной плазмы (см. §2), получаем ND~108 >> 1, и такая плазма является в высокой степени идеальной. Тогда как для плазмы линейной молнии, типичная температура которой составляет ~104 К, а концентрация примерно равна концентрации воздуха, ~1019 см-3, получаем ND~0,1. Такая плазма является слабонеидеальной, способной к рождению самоподдерживающихся нелинейных структур. Возможно, как полагают, именно такова природа шаровой молнии, возникающей часто при обычном грозовом разряде. Впрочем, детальный механизм этого природного явления пока окончательно не выяснен [С. К. Жданов, В. А. Курнаев, М. К. Романовский, И. В. Цветков. Основы физических процессов в плазме и плазменных установках].
§ 5. Прямые и обратные процессы в плазме
Ранее мы установили, что в газе-плазме могут происходить неупругие процессы: возбуждение частиц, диссоциация молекул, ионизация частиц. Очевидно, что должны быть и обратные процессы - снятие возбуждения тем или иным путем (такие процессы часто называют тушением), объединение атомов в молекулы (обычно такой процесс называют ассоциацией), объединение электронов и ионов (рекомбинация). Прямые и обратные процессы могут осуществляться различными путями: для прямых процессов необходимо сообщить частицам достаточную энергию, чтобы разорвать удерживающие их связи, при обратных процессах должен выделиться избыток энергии порядка энергии связи. При этом необходимо выполнение законов сохранения энергии и импульса. Рассмотрим эти процессы подробнее.
Возбуждение и тушение
Возбужденные состояния
возможны для всех сложных частиц – молекул, атомов, молекулярных и атомарных
ионов (кроме иона атома водорода). В молекулах и молекулярных ионах могут быть
возбуждены вращательные, колебательные и электронные состояния,
а в атомах и атомарных ионах – только электронные. С энергетической точки
зрения, наиболее легко возбуждаются вращательные уровни, труднее
колебательные, еще труднее электронные. Если принять за единицу расстояние
между электронными уровнями δEэ, то расстояние между колебательными
уровнями δEν, будет меньше в 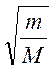 раз, а между
вращательными уровнями δEj еще меньше: в
раз, а между
вращательными уровнями δEj еще меньше: в ![]() раз, где М–масса
молекулы, a m–масса электрона.
раз, где М–масса
молекулы, a m–масса электрона.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.