Источники света. Тепловое излучение, страница 4

Приведя (4.22) к форме (4.18) определим вид универсальной функции F₂:

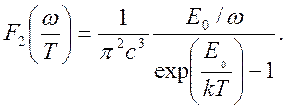                                                (4.23)

Чтобы выполнялся закон (4.18) E₀ должна быть пропорциональна частоте стоячей волны ω –  E₀=ħω, тогда функция F₂ становится зависящей от аргумента  ω/T. Тогда универсальная функция приобретает вид:

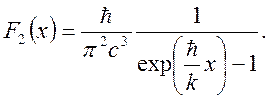                                                (4.24)

Но тогда коэффициент пропорциональности ħ=(1.0545887±0.0000057)_*10^-34 дж_*сек – универсальная постоянная – постоянная Планка. Выражение для плотности энергии теплового излучения теперь будет следующим:

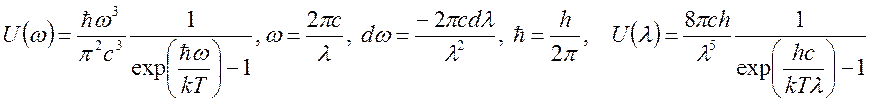                        (4.25)

В (4.25) при переходе от частот к длинам волн учтено, что dω=(2π/c)dλ/λ². В области низких частот или при постоянной Планка , стремящейся к нулю формула (4.25) переходит в формулу Рэлея-Джинса. В области высоких частот можно в формуле (4.25) можно пренебречь единицей - получается распределение Вина:

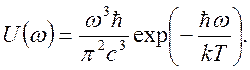                                                (4.26)

Распределение плотности энергии (4.25) можно проинтегрировать по всему спектру. В результате получим полную энергию теплового излучения:

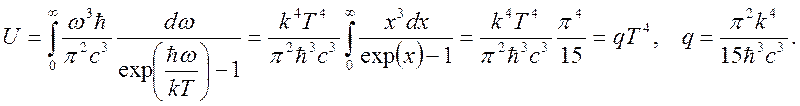          (4.27)

На практике более удобно использовать поверхностную светимость S, задающую поток излучения в полусферу с единичной площадки. Для АЧТ, подчиняющегося закону Ламберта S=πB=πI=cU/4. В результате, получим выражение для светимости АЧТ, выраженную через постоянную Стефана-Болцмана:

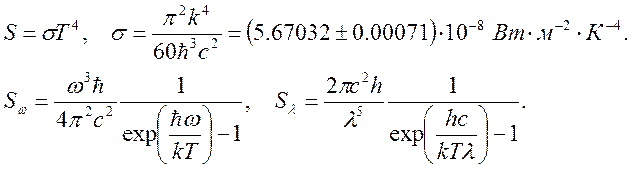                                      (4.28)

Функция S_λ достигает максимума при hc/kTλ=4.965, т.е. можно получить закон смещения Вина в виде Tλ= hc/4.965k=2.898*10^-3. Если λ [µ], то Tλ=2898.

Функция S_ω достигает максимума при ђω/kT = 2.821, что дает закон смещения вина в виде – ω/T=2.821*k/ђ=3.694*10¹¹. Для частоты, выраженной в обратных сантиметрах ν[см^‑1]/Т=1.961. Переход к ν[см^‑1] осуществляется с помощью выражения ν[см^‑1]=1/λ[см].

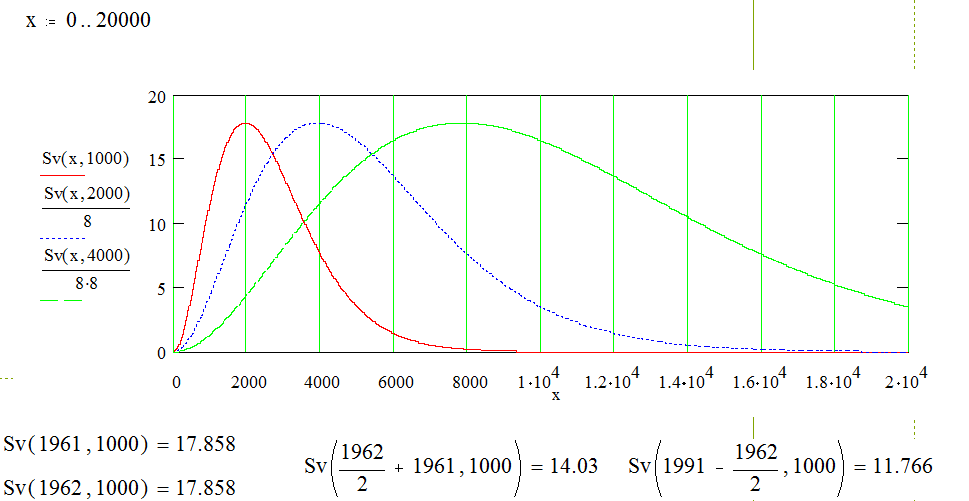
Распределение Планка было выведено Эйнштейном в предположении, что кроме спонтанных переходов существуют вынужденные, вероятность которых пропорциональна плотности лучистой энергии. Пусть имеем двухуровневый газ, находящийся в тепловом равновесии с излучением. Тогда на основе принципа детального равновесия можно написать уравнение баланса для переходов с верхнего уровня m на нижний - n и наоборот:

                                                                            (4.29)

Коэффициент A – определяет интенсивность спонтанных переходов, B – вынужденных, N – количество атомов в заданном состоянии. Интенсивность вынужденных переходов пропорциональна плотности лучистой энергии. Вероятности вынужденных переходов вверх и вниз одинаковы – это свойство атома. Отношение числа атомов в верхнем и нижнем состояниях подчиняется закону Больцмана. В результате получим:

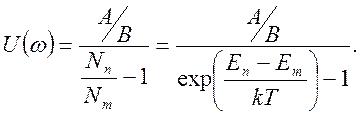                                                                                (4.30)

Полученное выражение по форме отвечает формуле Планка. Коэффициент A/B можно найти, сделав предельный переход в область высоких температур и применив формулу Рэлея-Джинса.

Модель АЧТ – сфера с маленьким отверстием, стенки которой при температуре T. Малая часть излучения выйдет обратно из сферы за счет отражения. Лампа накаливания. Глобар стержень из карбида кремния SiC (Tпл=2600⁰С, Tраб<1400⁰К, глобар с защитой из окиси тория ThO₂ - Tраб<2000⁰К) Для разжигания глобара требуется внешний подогрев. Степень черноты одинакова в широкой области спектра. Штифт Нернста – стержень из смеси ZrO₂, Y₂O₃, ThO₂ с глицерином с последующим спеканием с запеканием платиновых электродов. Платино-керамический излучатель с косвенным подогревом. Кратер угольной дуги. Тмах тепловых источников 4000⁰К, что определяет их спектральный диапазон.

Пирометрия, яркостная и цветовая температуры. Тярк = такой температуре черного тела, при которой их спектральные яркости равны.