Источники света. Тепловое излучение, страница 2

                                                           (4.5)

В (4.5) учтено, что коэффициенты отражения одинаковы для волн, идущих из вакуума в среду и из среды в вакуум. Производя сокращения получим:

                                                                  (4.6)

Закон преломления дает Sinφ_*n=Sinφ₀ и Cosφdφ_*n=Cosφ₀dφ₀, что приводит к соотношению

                                                         ,                                                         (4.7)

являющемуся математическим выражением закона Кирхгофа-Клаузиуса. Для получения соотношения для плотностей энергии (4.2) нужно еще учесть изменение групповой скорости:

                                                                                                                   (4.8)

Соотношения (4.7) и (4.8) справедливые для спектральных плотностей можно выразить через соотношения длин волн.

Изучим связь плотности энергии с температурой. Пусть изотропное излучение заключено в идеально отражающую оболочку, которую можно сжимать, расширять и  придавать ей любую температуру или теплоизолировать. Подвергнем излучение циклу Карно, состоящему из двух изотерм и двух адиабат. Прежде найдем связь светового давления с плотностью энергии. Давление – это плотность потока компоненты импульса,  перпендикулярной поверхности. импульс p_γ и энергия e_γ электромагнитного излучения связаны законом дисперсии p_γc=e_γ, Исходя из (4.1) найдем плотность потока импульса на стенку:

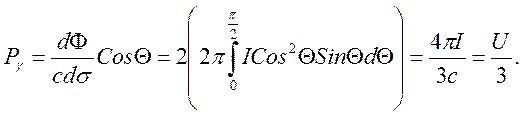                                                              (4.9)

В формуле учтено, что давление создается падающим на стенку и излученным потоками. Внутренняя энергия излучения E_i=UV. Работа P_γdV совершаемая при адиабатическом процессе равна изменению внутренней энергии dE_i. В результате, получим уравнение адиабаты:

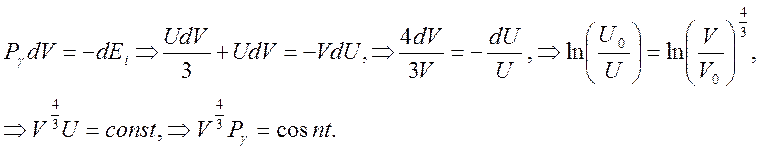                                  (4.10)

При изотермическом процессе энергия, складывающаяся из энергии изменения объема – UdV и механической работы – P_γdV, изменяется на количество тепла поступившего из термостата или отданного термостату (внутренняя энергия не меняется при T=const). Эта энергия пропорциональна абсолютной температуре:

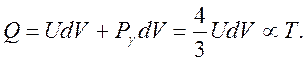                                             (4.11)

Схема цикла приведена на рисунке. На изотермических ветвях плотность энергии не меняется, поэтому отношение количеств тепла на ветвях 1-2 и 3-4 будет следующим:

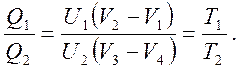                                                              (4.12)

На адиабатических ветвях имеет связь между  плотностью энергии и объемом в парах точек 2-3 и 1-4:

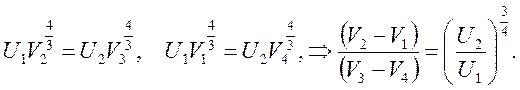                                                              (4.13)

Подстановка (4.13)  в  (4.12) дает:

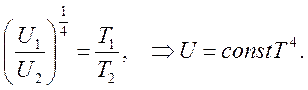                                                                  (4.14)

Последнее выражение – это математическая формулировка закона Стефана-Больцмана, а const в (4.14) – это универсальная постоянная, называемая постоянная Стефана-Больцмана.

Тепловое излучение, заключенное в оболочке с идеально отражающими стенками, будет оставаться равновесным при квазистатическом адиабатическом сжатии или расширении оболочки (Вильгельм Вин 1893-1894 г.). При адиабатическом сжатии оболочки будет совершена работа против сил светового давления и энергия излучения увеличится. Изменится и спектральный состав из-за эффекта Допплера. Чтобы излучение осталось равновесным достаточно ввести в объем бесконечно малую абсолютно черную пылинку. Сжимая или растягивая оболочку, можно получить равновесное излучение для разных объемов и, следовательно, температур. Выделим внутри сферической оболочки произвольный луч, падающий на стенку под углом Θ. Время между последовательными отражениями Δt=2r/cCosΘ. За это время радиус оболочки получит приращение Δr=vΔt. При каждом отражении происходит Допплеровский сдвиг частоты:

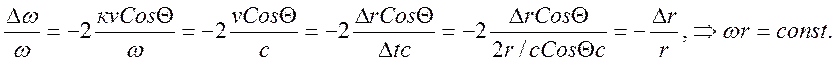                                 (4.15)