Источники света. Тепловое излучение, страница 3

Считая, что объем пропорционален r³, получим – ω³V=const, или, возводя в степень 4/3, получим – ω⁴/U=const. Учитывая связь энергии и температуры на основа6нии закона Стефана-Больцмана, получим соотношение:

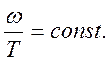                                                                                                            (4.16)

При адиабатическом сжатии и расширении спектральный состав меняется из-за эффекта Доплера для каждой спектральной компоненты независимо от других компонент, поэтому адиабатические инварианты (4.10) справедливы и для спектральных плотностей - U_ωdω. Тогда константой будет и величина U_ωdω/ω⁴. Поскольку свойства излучения зависят только от температуры, то излучение с такими же свойствами можно получить простым нагреванием, а все понятые закономерности сохранятся, т.к. они – свойство равновесного излучения. Изменим теперь температуру излучения любым способом, тогда в силу справедливости соотношения (4.16) для каждой спектральной компоненты можно написать dω/T= dω^//T^/ .Полученные инварианты позволяют прояснить функциональную зависимость U_ω(ω,T).  В силу инвариантности справедливы соотношения для спектральных плотностей при разных температурах:

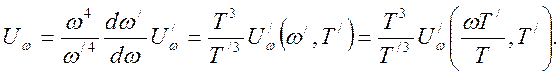                            (4.17)

Соотношение (4.17) справедливо при любой температуре T^/, поэтому правая часть не зависит от T^/. Формулу (4.17) можно переписать в виде:

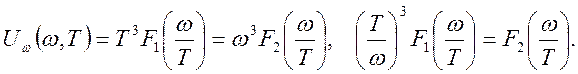                            (4.18)

Функции F₁(x) и F₂(x) – это универсальные функции имеющие максимум при некотором значении аргумента x=ω/T, следовательно,  максимум спектрального распределения плотности энергии  теплового излучения смещается линейно с ростом температуры – закон смещения Вина.

Для дальнейшего определения структуры спектрального распределения плотности энергии  теплового излучения требуется более детальной знание микроскопических процессов. Первый общий метод определения  U_ω  был выдвинут Рэлеем (1900 г.) и развит Джинсом (1905 г.). Их метод основывался на теореме классической стат. механики о равномерном распределении энергии по степеням свободы.  На каждую степень свободы приходится энергия 1/2kT , где k=1.38*10^-16 эрг/K – это постоянная Больцмана. Дальше задача сводится к вычислению степеней свободы. Для этого берем кубический объем с линейным размером – L. Решения волнового уравнения с нулевыми граничными условиями – это стоячие волны с такими импульсами, чтобы на размере объема укладывалось целое число полуволн. Разрешенные значения волновых векторов определяются соотношением q_jL=πm_j – (m_j – целые числа). Фазовый объем в импульсном пространстве, приходящийся  на одну волну определяется из условия Δm_j=1, следовательно (Δq_j)³=(π/L)³. Полный фазовый объем, занимаемый полем, определяется максимальным  положительным импульсом (октант от сферы):

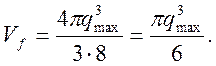                                                                                                        (4.19)

Полное число состояний Z=V_f/(Δq_j)³ , что дает возможность определить плотность состояний - dZ/dω*kT=U_ω*V и связанную с этой величиной плотность энергии:

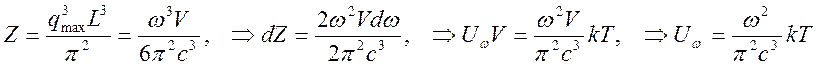                                        (4.20)

Плотность энергии, определяемая формулой (4.20) известна как закон Рэлея-Джинса, приводящий к ультрафиолетовой катастрофе. Устранялась ультрафиолетовая катастрофа в гипотезе Планка (1900 г.). Идея Планка состояла в том, чтобы каждой стоячей волне в нашем объеме приписать определенную энергию, которая складывается из порций E₀ и вероятность иметь энергию mE₀ подчиняется закону Больцмана – exp(-mE₀/kT).  В результате средняя энергия состояния равна не kT, а несколько иной величине:

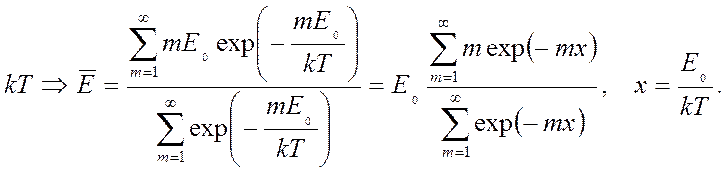                        (4.21)

Суммирование геометрической прогрессии дает значения для числителя и знаменателя (4.21) и величины средней энергии:

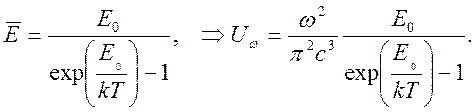                                                (4.22)