Измерение температуры термоэлектронов в вакуумном диоде, страница 6

1.  Оцените, при каких значениях R и I_нзапирание тока анода при прохождении тока накала катода будет эффективным. Оцените ошибку, вызванную недостаточным запиранием тока анода.

2.  Оцените изменение температуры нити катода за время, когда ток накала заперт диодом (7) (Рис.3).

3.  Как при U > j*  найти минимум потенциала j_min  для каждого потенциала анода?

6. Приложение

6.1.Теория потенциала для плоского диода. Приведем вывод основных формул, описывающих работу диода с нагретым катодом для плоского случая при ограничении тока диода пространственным зарядом электронов.

На поверхности катода функцию распределения электронов, покидающих катод, можно описать одномерным распределением Максвелла по нормальной к катоду компоненте скорости

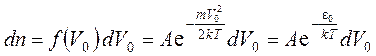 ,                                                            (11)

где  - их энергия и скорость на поверхности катода, n - объемная плотность электронов, , а нормировку определим через ток эмиссии с катода :

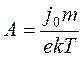,                                                                                 (12)

где m- масса электрона.

В режиме ограничения тока диода пространственным зарядом  j < j₀ в диодном зазоре Lс потенциалом анода Uна координате x_min формируется потенциальный барьер с минимумом потенциала j_min, возвращающий часть эмитированного тока обратно на катод (Рис.1). В диоде полная энергия электронов сохраняется , и поэтому, подставив e₀ в (11), запишем функцию распределения электронов по нормальной к поверхности катода компоненте скорости V на координате x с потенциалом j   

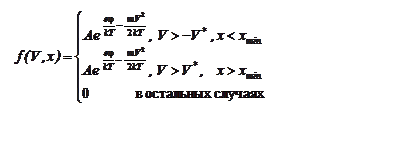
(13)

Здесь  - граничная скорость на координате x для электронов, преодолевших барьер.

Соответственно, плотность электронов в диодном промежутке имеет вид:

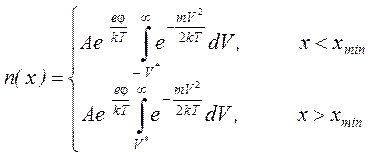                                                   (14)

Плотность тока диода определяется электронами, прошедшими потенциальный барьер и достигшими анода. Интегрируя функцию f(V,x)V на координате барьера x = x_min по скоростям V > 0, получим

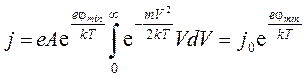,                                                                      (15)

что подтверждает формулу (2) для тока плоского диода.

Чтобы получить распределения потенциала по координате, рассмотрим сначала участок диода между катодом и потенциальным барьером 0 < x < x_min. Используя обозначения 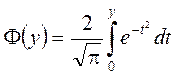 для интеграла ошибок и  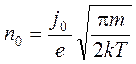для плотности электронов на катоде, эмитированных с его поверхности и имеющих нормальную компоненту скорости V > 0, перепишем выражение для плотности электронов в виде

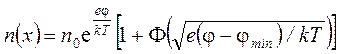,                                                       (16)

Для нахождения зависимости j(x) необходимо решить уравнение Пуассона

                                                                                  (17)

для этой области с граничными условиями

j(x=0) = 0, dj(x=x_min)/dx = 0.

Помножив уравнение (17) на dj/dx и проведя одно интегрирование по x от 0 до x_min, получим после подстановки второго граничного условия

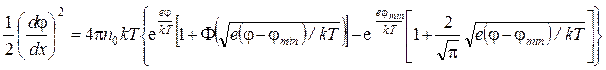                   (18)

Далее рассмотрим область между потенциальным барьером и анодом x_min < x < L. Для нее уравнение Пуассона имеет вид

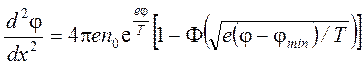                                                           (19)

с граничными условиями j(x_min) = j_min, dj(x_min)/dx = 0, j(L) = U. Заметим, что оно отличается от уравнения (17) с правой частью (16) только знаком перед интегралом ошибок. Аналогичным образом, после интегрирования от x_min до x, получаем

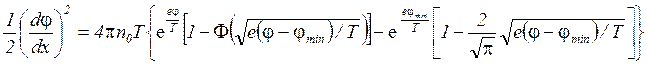(20)

Следуя обозначениям работы [10], определим безразмерный потенциал как

h = e(j-j_min)/kT,

а безразмерную длину как

x = 2b(x-x_min),

где §

 ,                                    (21)              ,

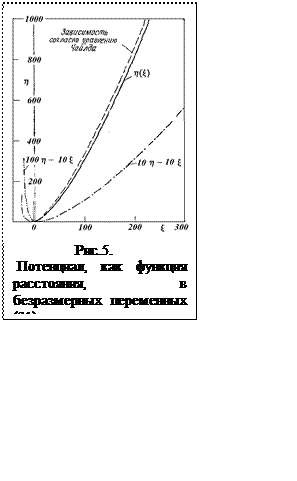
и, проинтегрировав уравнения (18) и (20) еще раз, запишем их общим выражением

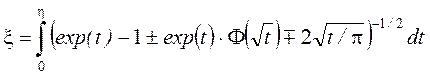.           (22)