Измерение температуры термоэлектронов в вакуумном диоде, страница 2

I  I₀exp(ej_min/kT).                (2)

Здесь e > 0 - элементарный заряд.

Зафиксируем температуру катода и ток эмиссии I₀ и будем уменьшать потенциал анода U относительно катода. Уменьшение потенциала U, как показано на Рис.1 (графики 3-6), приведет к увеличению величин -ej_min и x_min . Они возрастают до тех пор, пока координата минимума потенциала не достигнет анода x_min.= L(график 6). При этом "критическом" значении потенциала анода U= j* минимум потенциала сравнивается с ним, j_min(L)=j*.

Во всех случаях, показанных на Рис.1, при U > j* запирание тока диода определяется минимумом потенциала j_min, который достаточно сложно зависит и от тока накала, и от потенциала анода. Только в случае U < j* потенциалом, запирающим ток диода, является сам потенциал анода, и ток диода Iопределяется зависимостью I(U),которая для плоского диода имеет вид

I  I₀exp(eU/kT).                                                                                    (3)

Именно в этой области, изменяя потенциал анода, мы проведем исследование зависимости от него тока диода и определим температуру электронного газа в данной лабораторной работе.

2.2. Вольтамперная характеристика цилиндрического диода [6, 7].

Для анализа распределения по скоростям электронов, эмитированных с катода, достаточно изучить вольтамперную характеристику (ВАХ) диода в условиях, когда термоэлектронный ток на анод задерживается отрицательным напряжением анода, т.е., при U < j* < 0. Рассмотрим вакуумный диод с коаксиальными электродами, где катод прямого накала расположен по оси цилиндрического анода. Если радиус катода много меньше радиуса анода, можно считать, что начальные скорости электронов имеют составляющие только по оси цилиндра V_z  и по радиусу цилиндра V_r  (почему?). Силовые линии электрического поля направлены по радиусу цилиндра. Чтобы определить ток диода при отрицательных анодных напряжениях, надо вычислить интеграл

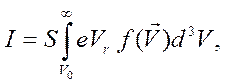                                                           (4)

где S - площадь катода, e > 0 – элементарный заряд.

Для расчётов удобно воспользоваться цилиндрической системой координат. В этой системе распределение Максвелла имеет вид

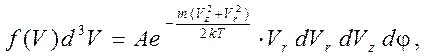                         (5)

(здесь j - азимутальный угол) а полный ток диода определяется выражением

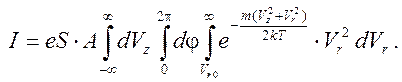                 `                       (6)

Здесь константу A определим из условия нормировки функции распределения, скорость V_r0 из  U  - величина запирающего (отрицательного) напряжения на аноде относительно катода.

После интегрирования по V_z и углу j получим, что ток диода прямо пропорционален интегралу

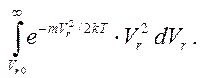                                                                           (7)

Произведя замену переменных  и, проинтегрировав по частям, получим

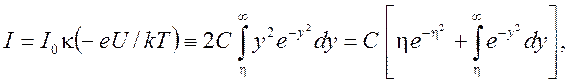                         (8)

где . Константу С можно получить из условия, что при отсутствии запирающего напряжения h=0 должен получиться полный ток эмиссии I₀:

                                                                                    (9)

Из выражения (8) температуру электронного газа (или катода) можно определить несколькими способами:

1)  построив график ВАХ в таких переменных, чтобы его вид определялся температурой электронов, как основным параметром и отсюда найти ее; - основное задание лабораторной работы;

2)  используя обратную к (8) функцию k^-1(I(U)/I₀)для графического определения температуры kT = - eU/[k^-1(I(U)/I₀)]из измеренного отношения I/I₀ для любой точки из ВАХ (предложено студентом ФФ И.Орловым [6]);

3)  численным дифференцированием ВАХ по потенциалу можно, как видно из (8), рассчитать подынтегральное выражение и даже выразить через него явный вид функции распределения электронов по энергиям. Такой метод на практике применяется довольно часто для произвольного вида f(V). Однако, из-за операции численного дифференцирования он в нашем случае значительно уступает по точности первым двум способам, поэтому здесь мы его рассматривать не будем.