Дифференцируемость функции. Дифференциал функции

9.5.      Дифференцируемость функции.  Дифференциал функции

1^°. Полным приращением функции  в точке , соответствующим приращениям аргументов , называется разность
                            .                  (5.1)

2^°.Функция f называется дифференцируемой в точке М, если существуют такие числа , что всюду в окрестности точки М полное приращение

функции можно представить в виде

,

где .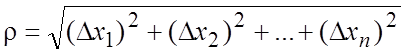

Теорема 9.3 (Необходимое условие дифференцируемости функции.) Если функция f дифференцируема во внутренней точке , то существуют частные производные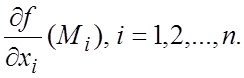

Теорема 9.4. (Достаточное условие дифференцируемости функции). Если частные производные 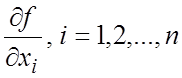 существуют и непрерывны во внутренней точке , то функция дифференцируема в М. Для дифференцируемой в точке М функции f  полное приращение
                                                        (5.2)

3^°. Дифференциалом df первого порядка функции  в точке  называется главная часть полного приращения (5.2), линейная относительно :

                                        .                       (5.3)

Подставив в (5.2) , получим  

l = 1,2,…,n  и  или . Тогда дифференциал функции f выражается через дифференциалы независимых переменных:

                                             .                     (5.4)

          Функции u и v нескольких переменных подчиняются обычным правилам дифференцирования:

              ,       ,    .      (5.5)

4^°.Дифференциалом 2-го порядка  функции  называется дифференциал от ее дифференциала 1-го порядка, рассматриваемого как функция переменных  при фиксированных (т.е. постоянных) :

.  Вообще,  дифференциал m – го порядка функции f:

                                                                                (5.6)

Пример 5. Найти полное приращение и дифференциал функции  в точке .

Ñ По формуле (5.1)  =.

          Дифференциал df есть главная часть полного приращения, линейная относительно :  .#

Пример 6. Найти дифференциал функции .

Первый способ. По формуле (5.4):  ,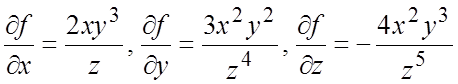

.

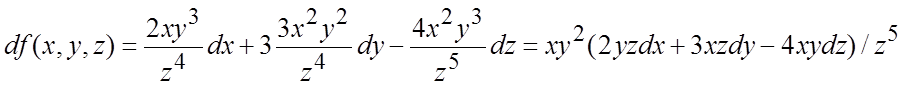Второй способ. Применяем правила дифференцирования (5.5):

+

. #

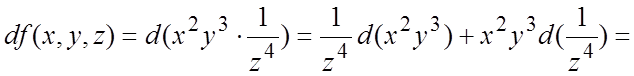
Пример 7. Найти дифференциалы 1-го, 2-го и 3-го порядков для функции .

Ñ По формуле (5.4):   . По формуле (5.6) при m = 2 и m = 3, считая dx и  dy постоянными, последовательно находим (смешанные частные производные не зависят от порядка дифференцирования):

=

#

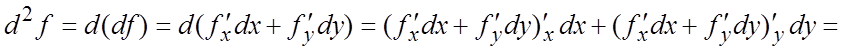
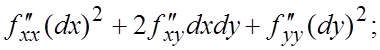
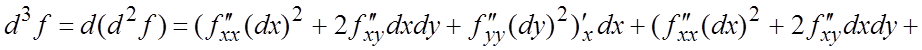
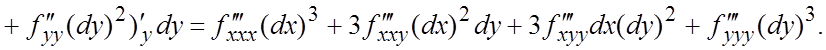Задачи для самостоятельного решения

Найти полное приращение и дифференциал функции z:

26. а) , если x изменяется от 2 до 2,1, а y – от 1 до 1,2.

       б) , если x изменяется от 2 до 2,1, а y – от 1 до 0,9.

Найти дифференциал функций:

27. 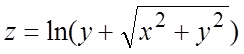.     28. .     29. .

30. Найти df(1,2,1), если .

Найти дифференциалы 1-го и 2-го порядков.

31. .     32. .     33. .

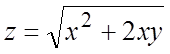34. .             35. .   35. .

9.6.      Дифференцирование сложных и неявных функций

9.6.1.   Сложные функции одной и нескольких переменных

1^°. Пусть  и в свою очередь, .

Теорема 9.5. Если функции  дифференцируемы в точке , то для производной сложной функции  одной переменной  справедлива формула

                                        или

                                       .                           (6.1)

          В частности, если t совпадает, например, с переменной , то  и “полная” производная функции и по  равна  

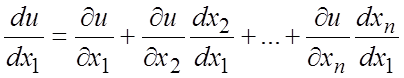                                          .                               (6.2)

2^°. Пусть  и, в свою очередь, , .

Теорема 9.6. Если функции  дифференцируемы в точке  , а функция f дифференцируема в точке , то сложная функция m переменных  дифференцируема в точке N и справедливы формулы:

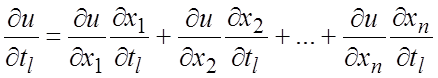
                                    ,         (6.3)

при этом частные производные функции u по  вычислены в точке М, а частные производные функций  по  (l=1,2,…,m) вычислены в точке N.

          Выражение для дифференциала 1-го порядка сохраняет вид (5.4) (свойство инвариантности формы первого дифференциала).

Пример 8. Найти , если , где .

Ñ По формуле (6.1) имеем    . #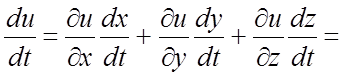

Пример 9. Найти производную функции .

Ñ Первый способ – применить логарифмическое дифференцирование, как делалось для функции одной переменной.

Второй способ. Функция u(t) есть результат образования сложной функции при подстановке в функцию  вместо x и y двух одинаковых функций переменой t:  . Тогда по формуле (6.1):  + получаем = 
+ .#

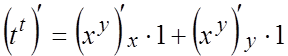Пример 10. Найти  и , если , где y = sin2x.

Ñ Имеем 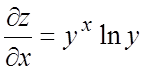. По формуле (6.2) получим = .#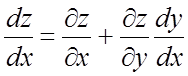

Пример 11. Найти 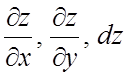, если , где , .

Ñ - сложная функция от независимых переменных x и y. Тогда по формулам (6.3) получим:    ;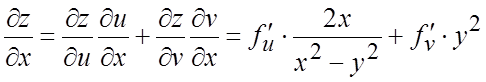

;  ,

,   ,

.#

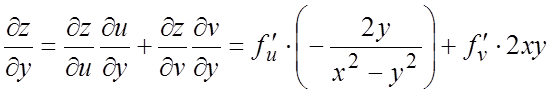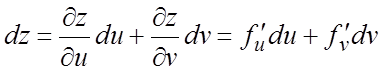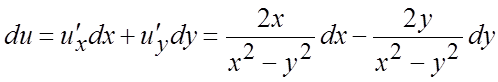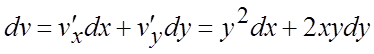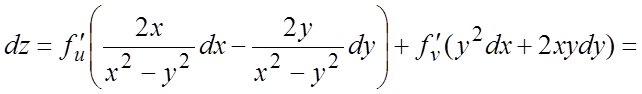
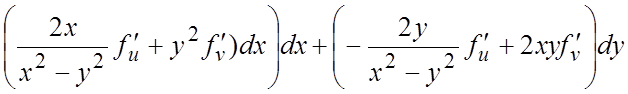9.6.2.   Неявные функции одной и нескольких независимых

переменных

1^°. Пусть дифференцируемая в точке x₀ функция y(x) задана неявно уравнением  и y=y(x) - решение этого уравнения. Если функция F дифференцируема, то производная функции y=y(x) определяется формулой

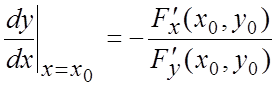                                                                                        (6.4)

при условии, что , где y₀ = y (x₀), F (x₀,y₀) = 0.

2^°. Пусть дифференцируемая в точке  функция  задана неявно уравнением  и u = - решение этого уравнения.

Если F дифференцируема, то частные производные функции u = в точке М ⁰ определяются по формулам

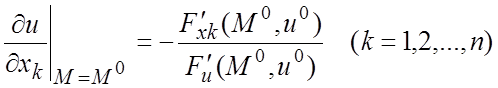                                                             (6.5)

при условии, что , где .

Пример 12. Найти , если .

Ñ  и по формуле (6.4) получаем 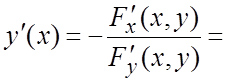 =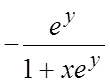. В нашем случае x₀ = 0. Непосредственной подстановкой убедимся, что точка  принадлежит графику функции, т.е. . Поэтому .#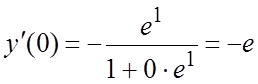

Пример 13. Найти 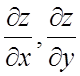, если .

ÑЛевую часть данного уравнения обозначим . По формуле (6.5) получим:, .#

Задачи для самостоятельного решения

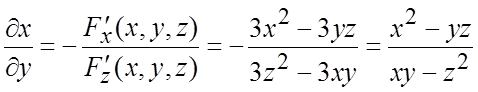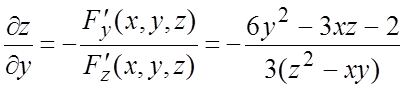37. Найти , если  где , .

38. Найти , если , где x = ln t, y = sin t.

39. Найти , если    где  .

40. Найти  и , если , где .

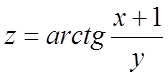41. Найти   и , если , где .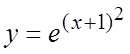

42. Найти , если , где .

43. Найти dz, если , где .