





ЛЕКЦИЯ
Диспергирующие элементы спектральных приборов. ПРИЗМА.
 |
 Призма – многогранник из прозрачного вещества с
основанием в виде треугольника. Для применения призмы в качестве
диспергирующего элемента необходимо наличие дисперсии показателя преломления – dn/dl¹0.
Требования на материал призмы – это прозрачность, однородность, большое
значение dn/dl, изотропность, технологичность, дешевизна. В УФ
области спектра применяется кварц, в видимой – стекло флинт (ТФ), в ИК области
– LiF (2 – 5 мкм), NaCl (0.5 – 15 мкм прибор СПМ-2), KBr (15 – 25 мкм).
Обычно размер основания призмы не больше 10 см. Существуют жидкостные призмы в
сосуде призматической формы.
Призма – многогранник из прозрачного вещества с
основанием в виде треугольника. Для применения призмы в качестве
диспергирующего элемента необходимо наличие дисперсии показателя преломления – dn/dl¹0.
Требования на материал призмы – это прозрачность, однородность, большое
значение dn/dl, изотропность, технологичность, дешевизна. В УФ
области спектра применяется кварц, в видимой – стекло флинт (ТФ), в ИК области
– LiF (2 – 5 мкм), NaCl (0.5 – 15 мкм прибор СПМ-2), KBr (15 – 25 мкм).
Обычно размер основания призмы не больше 10 см. Существуют жидкостные призмы в
сосуде призматической формы.
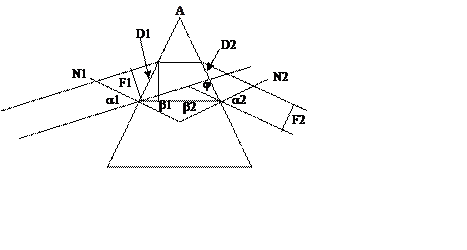
Преломление в плоскости главного сечения. Плоскость, перпендикулярная ребру AB, проходящая через середину ребра AB - главное сечение призмы. Рассмотрим преломление луча в плоскости главного сечения. Угол падения на боковую грань - a1, угол выхода луча - a2, угол при вершине призмы – A. Показатель преломления призмы – n. Ищем угол отклонения - j. На основании теорем элементарной геометрии можно написать следующие уравнения:
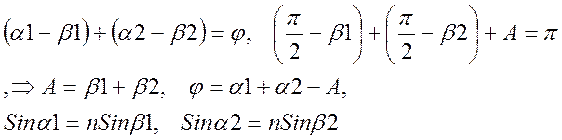 (1)
(1)
Пользуясь тригонометрическими формулами можно получить выражение для угла преломления:
|
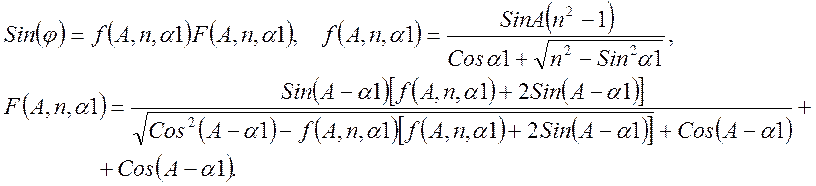 Из
выражения (2) легко видеть, что увеличение отклонения луча происходит при
увеличении угла A при вершине призмы и при увеличении показателя
преломления (n>1). Функция f(A,n,
a1) – пропорциональна
синусу преломляющего угла A и
отклонению показателя преломления от 1. Главным образом она и определяет дисперсионные
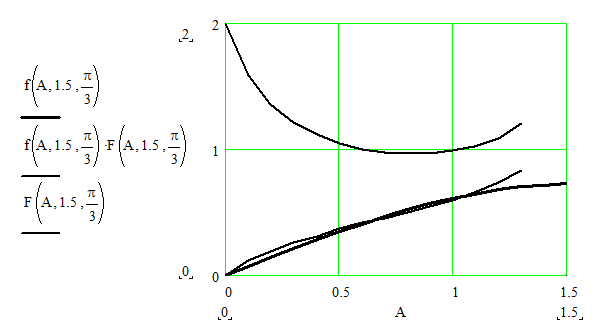
и угловые характеристики спектрального прибора. Функция F(A,n,
a1) более
пологая характеризует детали преломления. При A=0 или n=1, что
очевидно преломления луча не происходит. Можно найти также выражения для угла -
a2 выхода
луча из выходной грани:
Из
выражения (2) легко видеть, что увеличение отклонения луча происходит при
увеличении угла A при вершине призмы и при увеличении показателя
преломления (n>1). Функция f(A,n,
a1) – пропорциональна
синусу преломляющего угла A и
отклонению показателя преломления от 1. Главным образом она и определяет дисперсионные
и угловые характеристики спектрального прибора. Функция F(A,n,
a1) более
пологая характеризует детали преломления. При A=0 или n=1, что
очевидно преломления луча не происходит. Можно найти также выражения для угла -
a2 выхода
луча из выходной грани:
![]() (3)
(3)
 |
![]()
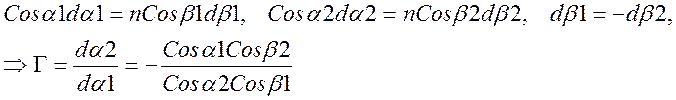 (4)
(4)
Нетрудно убедиться, что угловое увеличение напрямую связано с изменением ширины выходного пучка - F1/F2=-Г. Угловое увеличение может меняться от 0 до -¥. Очевидно применение маленьких или больших угловых увеличений не выгодно из-за потери предельной разрешающей способности, определяемой сечением пучка, пропорциональной минимальной из F1 или F2. Найдем условия наименьшего отклонения выходного пучка:
![]()
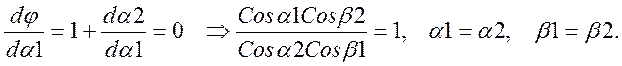 (5)
(5)
Угол наименьшего отклонения отвечает симметричному ходу луча и угловому увеличению, равному единице и одинаковым сечениям входного и выходного пучков. При этом углы преломления b1=b2=A/2. Предельный угол падения найдем из условия максимального угла выхода луча (Sin(a2)=1):
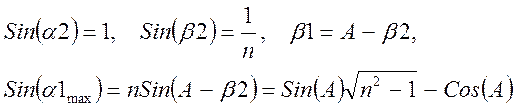 (6)
(6)
Дисперсия призмы связана с дисперсией показателя преломления.
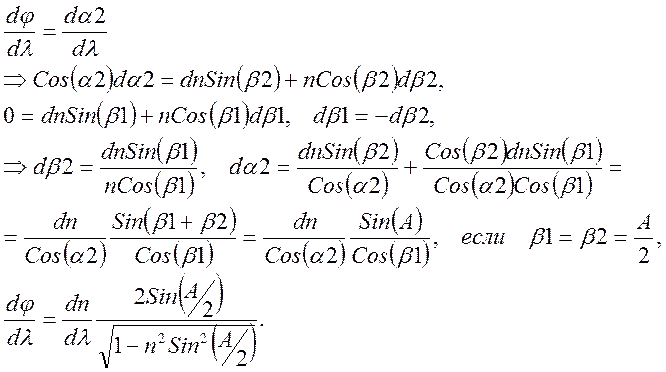 (7)
(7)
Формула (7) дают ограничение е для максимального преломляющего угла Sin(Amax/2)=1/n. Для n=1.5 Amax=83.6 град.
Предельная разрешающая способность призмы, как уже говорилось будет при максимально возможном заполнении призмы светом (F2 = max). Тогда, F2/Cos(a2) равно боковой стороне призмы. При умножении длины боковой стороны на синус половинного угла при вершине и удваивая это произведение, получим длину основания призмы:
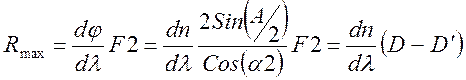 (8)
(8)
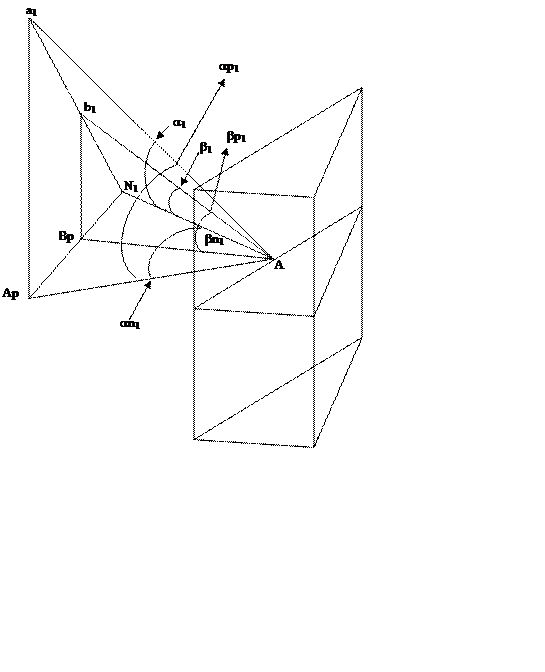 Искажения
призмой формы спектральных линий. При конечных размерах входной щели по
вертикали крайние лучи нельзя рассматривать как преломляемые призмой в главной
плоскости. Рассмотрим преломление призмой луча, пересекающего главную плоскость
под некоторым углом. Падающий луч – a1A, преломленный луч (продолжение) –b1A, N1 – нормаль
к поверхности призмы, ApA – проекция падающего луча, BpA– проекция
преломленного луча, a1AP, b1Bp -
перпендикуляры на плоскость главного сечения, плоскость a1ApN1, перпендикулярная
плоскости главного сечения выбрана перпендикулярной нормалиN1, an1 и bn1 – углы между
проекциями падающего и преломленного лучей в плоскости главного сечения и
нормалью N1, ap1 и bp1 – углы между падающим и преломленным лучами и их
проекциями, фактически – это углы между лучами и плоскостью, параллельной
главному сечению призмы.
Искажения
призмой формы спектральных линий. При конечных размерах входной щели по
вертикали крайние лучи нельзя рассматривать как преломляемые призмой в главной
плоскости. Рассмотрим преломление призмой луча, пересекающего главную плоскость
под некоторым углом. Падающий луч – a1A, преломленный луч (продолжение) –b1A, N1 – нормаль
к поверхности призмы, ApA – проекция падающего луча, BpA– проекция
преломленного луча, a1AP, b1Bp -
перпендикуляры на плоскость главного сечения, плоскость a1ApN1, перпендикулярная
плоскости главного сечения выбрана перпендикулярной нормалиN1, an1 и bn1 – углы между
проекциями падающего и преломленного лучей в плоскости главного сечения и
нормалью N1, ap1 и bp1 – углы между падающим и преломленным лучами и их
проекциями, фактически – это углы между лучами и плоскостью, параллельной
главному сечению призмы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.