Диспергирующие элементы спектральных приборов. Призма, страница 2

Согласно законам преломления, aA, bA, N₁A  - лежат в одной плоскости. Соответствие между углами a₁ и b₁ подчиняется закону Снелиуса (1). Треугольники  a₁AN₁, b₁AN₁, AApN₁, ABpN₁ - прямоугольные с прямым углом при вершине N₁, треугольники a₁ApA и a₁ApN₁, b₁BpA и b₁BpN₁ прямоугольные с прямыми углами при вершинах Ap и Bp. треугольники a₁ApN₁ и b₁BpN₁- подобны. Можно написать следующие соотношения для углов падения и преломления:

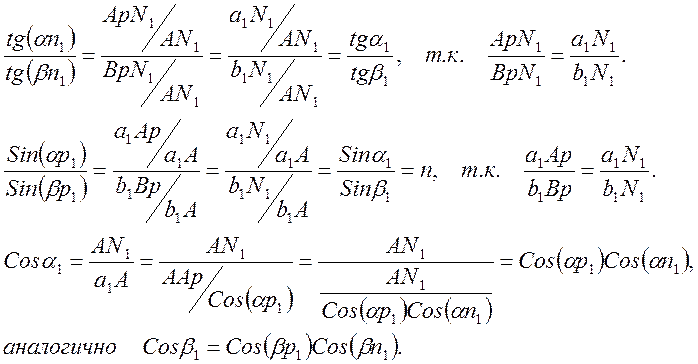                                                                                                                             (9)

Общий ход луча через призму теперь можно разложить на две составляющие – ход проекций луча в главном сечении и преломление луча не в плоскости падения, в плоскости a₁ApA, содержащей падающий луч и проекции его на главное сечение. Обратим внимание, что закон преломления луча в плоскости a₁ApA не зависит от угла наклона этой плоскости по отношению к плоскости призмы - an₁ (вторая строчка (9)). Поэтому для луча прошедшего сквозь призму (в силу перпендикулярности входной и выходной плоскости призмы главному сечению) можно сразу написать:

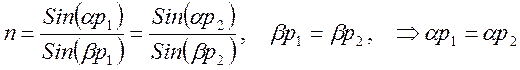                                                                                                                             (10)

Таким образом после преломления призмой неизменным остается угол между лучом (падающим и преломленным) и плоскостью, параллельной главному сечению. В плоскости, параллельной главному сечению, для закона преломления получаются соотношения:

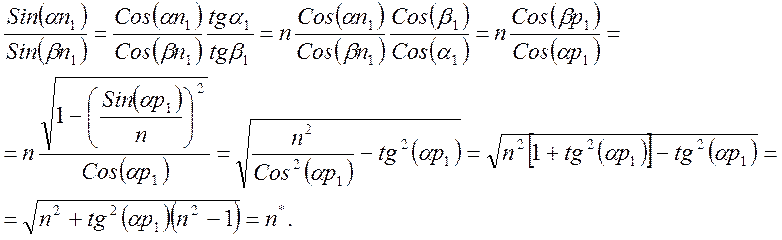 (11)

Преломление в призме проекции косого луча подобно преломлению луча в главном сечении если ввести эффективный показатель преломления n*, зависящий от угла падения луча на плоскость главного сечения. n* увеличивается с увеличением угла падения, что приводит к увеличению угла отклонения j. Максимальное  значение tg(ap₁)=h₁/2f₁ остается для большинства приборов много меньше 1.

Найдем изменение угла отклонения в зависимости от ap₁: Исходя из выражений (7) и (11), для монохроматического излучения можно написать:

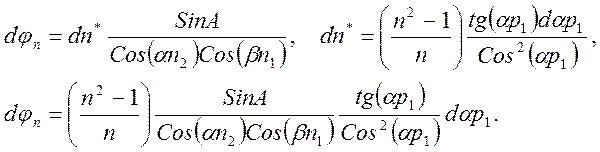                                                                                                                             (12)

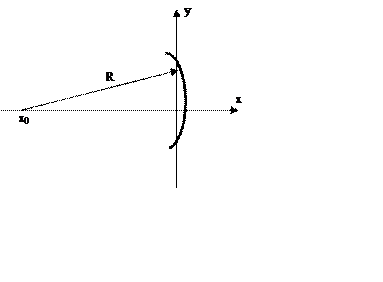В (12) применено разложение (11) по tg(ap₁) при ap₁=0. Угол отклонения не является пропорциональным углу ap₁, поэтому должна наблюдаться кривизна линий. Найдем радиус кривизны изображения входной щели. Пусть изображение щели – часть дуги окружности. Уравнение окружности в выбранной системе координат будет следующим:

                    (13)

Дифференциальное уравнение окружности при большом радиусе кривизны – x-x₀@R будет иметь вид:

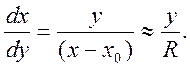                (14)

Горизонтальное отклонение dx=f₂d(an₂) = f₂d(j_n)   определяется изменением угла отклонения. Вертикальное отклонение задается углом падения .

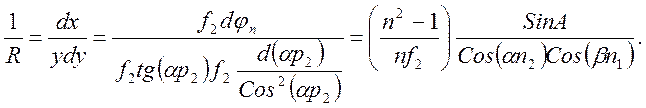                                                                                                                             (15)

При установке призмы в положение минимального отклонения из (15) и (7) для луча в главном сечении следует выражение:

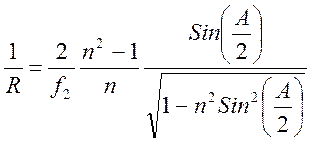                                                                                                                             (16)

Выражение (16) используется для оценки кривизны изображения спектральных линий.

При падении на призму непараллельного (сходящегося или расходящегося) пучка лучей в силу различия законов преломления в меридиональной и саггитальной плоскостях происходит изменение структуры пучка. В результате возникает астигматизм. Для астигматической разности имеется формула:

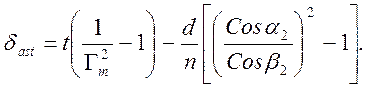                                                                                                                             (17)

t – расстояние от точки падения лучей на призму до точки схождения (фокуса) продолжения лучей, Г_m – меридиональное угловое увеличение, d – путь осевого луча в призме. Астигматизм вреден при одновременной кривизне изображения спектральных линий.

Разный коэффициент пропускания призмы при изменении длины пути в призме также приводит к искажениям формы изображения спектральных линий и потере разрешающей способности из- за эффективного уменьшения действующей апертуры призмы. Для устранения этого эффекта ценой потери светосилы применяют фигурные диафрагмы.

Для устранения изменения углового увеличения при сканировании спектра применяют системы постоянного отклонения. Идея таких систем состоит в одновременном изменении угла падения и  угла преломления с тем чтобы для выделяемых длин волн угловое угол отклонения всегда оставался постоянным. при этом увеличение остается  равным 1.  Наибольшее распространение получила призма Аббе с углом отклонения 90⁰. 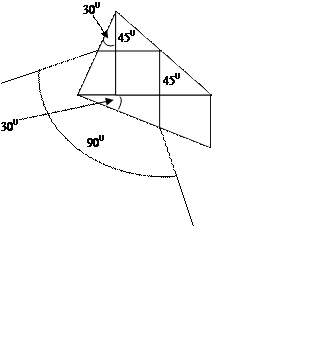Простая призма Аббе (выполняется из целого куска оптического стекла) состоит фактически из двух преломляющих призм A=30⁰ и поворотной 90⁰ призмы . Часто для уменьшения поглощения применяют составную призму Аббе, в которой диспергирующие призмы выполнены из флинта, а поворотная из крона. 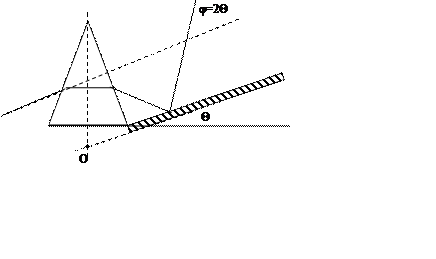Более простые системы постоянного отклонения можно построить из призмы и плоского зеркала  - системы Водсворта. Сканирование спектра осуществляется поворотом вокруг точки O.  Распространены автоколлимационные системы на основе полупризмы Литтрова.