Взаимодействие излучения с веществом, вероятности переходов (Глава 2 учебного пособия)

2. Взаимодействие излучения с веществом, вероятности переходов

Нашей задачей является исследование переходов в атомной системе, связанных с излучением и поглощением фотонов. Рассмотрим  фотонов с импульсом  и поляризацией , находящихся в объеме V. Атомы считаем невзаимодействующими между собой. Взаимодействие фотонов с атомами будем рассматривать в рамках полуклассической теории, в которой атомы являются квантовой системой, а внешнее электромагнитное поле описывается уравнением Максвелла и представляет собой заданную функцию координат и времени. Предполагается, что поле достаточно интенсивно , чтобы можно было пренебречь обратным влиянием системы атомов на поле – изменением поля в результате поглощения или испускания одного кванта. При этом, однако, поле не настолько сильно, чтобы возникла необходимость учитывать квадратичные члены теории возмущений

В этом случае взаимодействие фотона с атомом можно описать методами линейной теории возмущений [1, 2]. Рассмотрим наиболее часто встречающийся случай, когда при  атом находился в определенном состоянии i, а при  на него действует слабое периодическое возмущение с частотой . Энергия начального состояния , а конечного – . Вероятность перехода за единицу времени в бесконечно малый интервал конечных состояний с квантовыми числами от , до  (среди которых есть и энергия ) равна

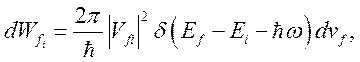                                   (2.1)

где  – матричный элемент от потенциала взаимодействия.

Наличие дельта-функции в (2.1) отражает выполнение условия сохранения энергии: система испускает  или поглощает  квант электромагнитного поля, переходя в конечное состояние f. Если состояние f полностью характеризуется энергией, то  и полная вероятность перехода :

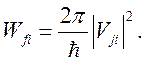                                                (2.2)

В большинстве случаев конечные состояния вырождены, что особенно типично для непрерывного спектра. Тогда вводится плотность конечных состояний  на единичный интервал энергий, т.е. :

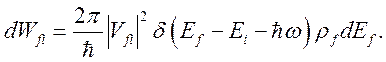                                   (2.3)

После интегрирования по энергиям из (2.3) получим:

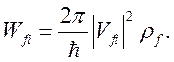                                           (2.4)

2.1. Определение плотности конечных состояний

Явное выражение  зависит от нормировки состояний f непрерывного спектра. Они должны быть нормированы на -функцию от переменных .

В нашем случае  определяется статвесом атома в конечном состоянии ; статвесом фотонов , определяемом двумя направлениями их поляризации; плотностью конечных состояний фотонов в пространстве :

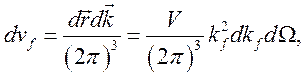                                   (2.5)

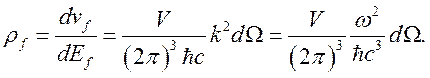                             (2.6)

Учитывая, что нас интересует излучение (поглощение) фотонов независимо от их поляризации, то полная величина  равна

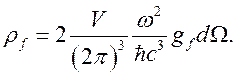                                        (2.7)

2.2. Оценка величины матричного элемента

Используем эффективное дипольное взаимодействие атома с моментом с электромагнитной волной:

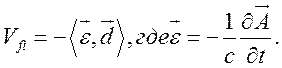
Представим векторный потенциал  падающей волны в виде суперпозиции Фурье-гармоник 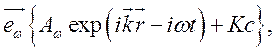где  – вектор поляризации, Kc – комплексно сопряженное первого слагаемого. Тогда

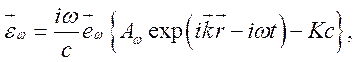
Энергия волны равна

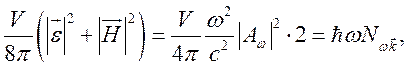                            (2.8)

где  – число фотонов в объеме V с частотой  и волновым вектором . Следовательно,

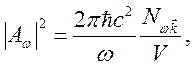
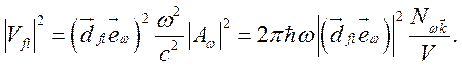                          (2.9)

Из (2.9), (2.4) и (2.7) получим

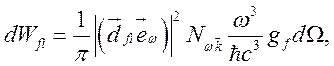                              (2.10)

где  – элемент телесного угла, характеризующий направление волнового вектора . Усредняя по величине угла между векторами  и  и суммируя по двум поляризациям фотонов, для случая неполяризованного света, получим окончательное выражение:

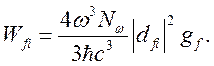                                   (2.11)

Индекс  у числа фотонов  в дальнейшем будем опускать.

Результат (2.11) означает наличие бесконечно узкой линии поглощения. Однако мы знаем, что в силу конечности времени жизни возбужденное состояние обладает конечной шириной . Если падающая волна имеет разброс по частотам , то возможны переходы с сохранением энергии во все монохроматические компоненты возбужденного состояния. Мы должны в (2.3)  заменить на

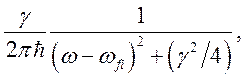
где  и

Таким образом, получим естественную форму линии:

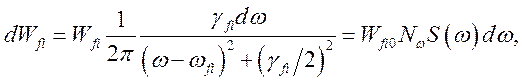           (2.12)

где  – нормированная на единицу ширина уровня.

Подставляя в выражение для в качестве  пренебрегая , учитывая, что и сравнивая с (1.2), получим, что величина  т.е. равна вероятности спонтанного перехода в единицу времени с уровня I на уровень f.

Учитывая, что 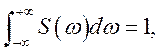 величина  характеризует полную вероятность перехода под действием поля излучения. Причем вероятность поглощения  и вынужденного испускания  связаны соотношением

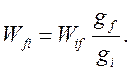                                              (2.13)

Здесь предположено, что уровень f энергетически ниже уровня i.